题目内容
9.“a=-1”是方程“a2x2+(a+2)y2+2ax+a=0表示圆”的( )| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分有不必要条件 |
分析 由题意可得:把方程a2x2+(a+2)y2+2ax+a=0化简整理可得:a2(x+$\frac{1}{a}$)2+(a+2)y2=1-a,结合题意可得a2=a+2,并且1-a>0,再根据充要条件的定义即可判断.
解答 解:由题意可得:把方程a2x2+(a+2)y2+2ax+a=0化简整理可得:a2(x+$\frac{1}{a}$)2+(a+2)y2=1-a,
因为此曲线表示圆,
所以a2=a+2,并且1-a>0,
所以解得:a=-1.
故“a=-1”是方程“a2x2+(a+2)y2+ax+a=0表示圆”的充要条件,
故选:A.
点评 本题主要考查二元二次方程与圆的对应关系,解决此类问题的关键是熟练掌握圆的方程,以及学生要有较强的运算能力.

练习册系列答案
相关题目
4.设曲线f(x)=$\frac{x}{lnx}$在点P(x,f(x))处的切线在y轴上的截距为b,则当x∈(1,+∞)时,b的最小值为( )
| A. | e | B. | $\frac{e}{2}$ | C. | $\frac{{e}^{2}}{2}$ | D. | $\frac{{e}^{2}}{4}$ |
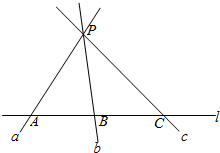 如图,过直线l外一点P,作直线a,b,c分别交直线l于点A,B,C,求证:直线a、b、c共面.
如图,过直线l外一点P,作直线a,b,c分别交直线l于点A,B,C,求证:直线a、b、c共面.