题目内容
14.在△ABC中,a,b,c分别是角A,B,C的对边,且4cosC•sin2$\frac{C}{2}$+cos2C=0.(Ⅰ)若函数f(x)=sin(C-2x),求f(x)的单调增区间;
(Ⅱ)若3ab=-25-c2,求△ABC面积的最大值.
分析 (1)利用已知等式,通过二倍角的余弦函数化简,求出C的余弦值,得到C的大小,化简函数f(x)=sin(C-2x),利用正弦函数的单调性,求f(x)的单调增区间;
(2)利用3ab=25-c2,由余弦定理:c2=a2+b2-2abcosC,25-3ab=a2+b2-ab,求出(a+b)2=5,利用基本不等式求解面积的最大值.
解答 解:(1)由条件:4cosC•$\frac{1-cosC}{2}$+2cos2C-1=0,∴cosC=$\frac{1}{2}$
故C=$\frac{π}{3}$,则f(x)=sin($\frac{π}{3}$-2x),
∴$\frac{π}{2}$+2kπ≤2x-$\frac{π}{3}$≤$\frac{3}{2}$π+2kπ
∴$\frac{5π}{12}$+kπ≤x≤$\frac{11}{12}$π+kπ,k∈Z
∴f(x)的单调增区间为[$\frac{5π}{12}$+kπ,$\frac{11}{12}$π+kπ]k∈Z
(2)由余弦定理:c2=a2+b2-2abcosC
∴25-3ab=a2+b2-ab,
∴(a+b)2=25,
∴a+b=5,
∴S△ABC=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{4}$ab≤$\frac{\sqrt{3}}{4}•(\frac{a+b}{2})^{2}$=$\frac{25\sqrt{3}}{16}$,
当且仅当a=b=$\frac{5}{2}$取得最大值$\frac{25\sqrt{3}}{16}$.
点评 本题考查二倍角的余弦函数,余弦定理,正弦函数的单调性,三角形的面积以及基本不等式的应用,考查计算能力.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
2.已知集合A={x|$\frac{1}{x-2}<1$},B={x||x-1|≤2},则A∩B=( )
| A. | (-∞,1)∪[2,3) | B. | [-1,2) | C. | (-∞,-1)∪[2,3)∪(3,+∞) | D. | (-∞,-1)∪(3,+∞) |
9.“a=-1”是方程“a2x2+(a+2)y2+2ax+a=0表示圆”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分有不必要条件 |
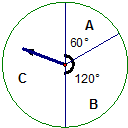 五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右上表.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右上表.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.