题目内容
1．
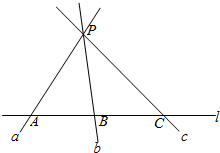如图，过直线l外一点P，作直线a，b，c分别交直线l于点A，B，C，求证：直线a、b、c共面．
分析 先设直线l与l外一点P确定一个平面α，再证明直线a?平面α，同理得出直线b、c?平面α即可．
解答 证明：设直线l与l外一点P确定的平面为α，
则P∈平面α，
又A∈直线l，∴A∈平面α；
又P∈直线a，A∈直线a，
∴直线a?平面α；
同理直线b?平面α，直线c?平面α，
∴直线a、b、c共面．
点评 本题考查了空间中的三线共面问题，也考查了逻辑推理与证明能力，是基础题目．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
9．“a=-1”是方程“a2x2+（a+2）y2+2ax+a=0表示圆”的（ ）
| A． | 充要条件 | B． | 充分不必要条件 | ||
| C． | 必要不充分条件 | D． | 既不充分有不必要条件 |
16．根据下面某工程的工作明细表：
（1）画出工作流程图；
（2）指出关键路径；
（3）确定完成工程的最短总工期．
| 工作代码 | 紧前工作 | 工期（天） |
| A | 无 | 7 |
| B | 无 | 3 |
| C | 无 | 1 |
| D | C | 3 |
| E | A，B，D | 3 |
| F | E | 2 |
| G | A，B，D | 2 |
| H | F，G | 1 |
（2）指出关键路径；
（3）确定完成工程的最短总工期．
11．已知函数y=f（x）的图象过点（1，2），则y=f（x+1）的图象过点（ ）
| A． | （1，2） | B． | （2，2） | C． | （0，2） | D． | （-1，2） |