题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,已知椭圆
,已知椭圆![]() 上存在点
上存在点![]() ,使
,使![]() ,且这样的点
,且这样的点![]() 有且只有两个.
有且只有两个.
(1)求椭圆![]() 的离心率;
的离心率;
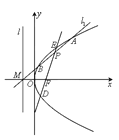
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,
,![]() 是坐标原点,求
是坐标原点,求![]() 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)利用椭圆的对称性可知满足条件的点![]() 有且只有两个,则点
有且只有两个,则点![]() 位于椭圆的上下顶点,则根据椭圆的几何性质求解即可;
位于椭圆的上下顶点,则根据椭圆的几何性质求解即可;
(2)设直线![]() ,椭圆的方程为
,椭圆的方程为![]() ,二者联立可得
,二者联立可得![]() ,且
,且![]() ,根据韦达定理可得
,根据韦达定理可得![]() ,由
,由![]() 可得
可得![]() ,即
,即![]() ,代入
,代入![]() 中,再利用均值定理求解可得
中,再利用均值定理求解可得![]() ,代回求得点
,代回求得点![]() ,进而求得
,进而求得![]() 即可.
即可.
解:(1)由题,根据椭圆的对称性可知,满足条件的点![]() 有且只有两个,
有且只有两个,
则点![]() 位于椭圆的上下顶点,
位于椭圆的上下顶点,
则离心率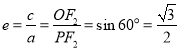
(2)易知直线![]() 不与
不与![]() 轴重合,设
轴重合,设![]() ,
,![]() ,
,![]() ,
,
由(1),因为![]() ,所以
,所以![]() ,所以设椭圆的方程为
,所以设椭圆的方程为![]() ,
,
联立![]() ,消去
,消去![]() 可得
可得![]() ,
,
则![]() ,即
,即![]() ①
①
所以![]() ②
②
因为![]() ,所以
,所以![]() ,
,
代入②式可得![]() ,
,
所以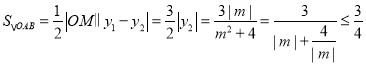 ,
,
当且仅当![]() ,即
,即![]() 时,
时,![]() 的面积有最大值,
的面积有最大值,
不妨令![]() ,则
,则![]() ,
,![]() ,代入
,代入![]() ,可得
,可得![]() ,满足①式,
,满足①式,
故椭圆的方程为![]() .
.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目