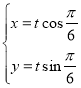题目内容
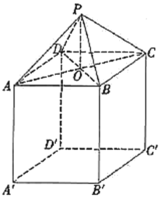
【题目】如图所示，一个仓库设计由上部屋顶和下部主体两部分组成，屋顶的形状是四棱锥
，四边形
是正方形，点
为正方形的中心，
平面；下部的形状是长方体
.已知上部屋顶造价与屋顶面积成正比，比例系数为
，下部主体造价与高度成正比，比例系数为
.若欲造一个上、下总高度为10
,
的仓库，则当总造价最低时，
（ ）
A.
B.
C.4D.
【答案】B
【解析】
取
的中点为
，表示OE，由于
平面
，在
中，设
，表示
，
，从而分别表示上部屋顶面积，下部主体的高度，进而表示仓库的总造价的函数关系，利用求导分析单调性，再求得最小值，即为答案.
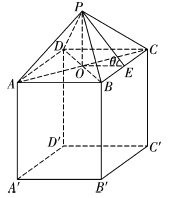
如图，设的中点为，连接
，则
.
由于平面，则有
；
在中，设，则有
，
，
所以上部屋顶面积为
，下部主体的高度为
，
所以仓库的总造价为
.
设
，所以
.令
，得
，所以
；
则当
时，
，
在
上单调递减；
当
时，
，在
上单调递增；
所以当时，有最小值，此时
，
故选：B
名校课堂系列答案
【题目】某果园种植“糖心苹果”已有十余年，根据其种植规模与以往的种植经验，产自该果园的单个“糖心苹果”的果径（最大横切面直径，单位：
）在正常环境下服从正态分布
.
（1）一顾客购买了20个该果园的“糖心苹果”，求会买到果径小于56的概率；
（2）为了提高利润，该果园每年投入一定的资金，对种植、采摘、包装、宣传等环节进行改进.如图是2009年至2018年，该果园每年的投资金额
（单位：万元）与年利润增量
（单位：万元）的散点图：
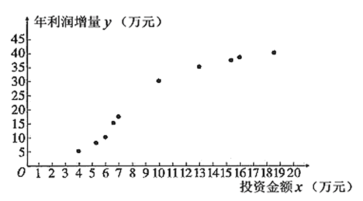
该果园为了预测2019年投资金额为20万元时的年利润增量，建立了关于的两个回归模型；
模型①：由最小二乘公式可求得与的线性回归方程：
；
模型②：由图中样本点的分布，可以认为样本点集中在曲线：
的附近，对投资金额做交换，令
，则
，且有
，
，
，
.
（I）根据所给的统计量，求模型②中关于的回归方程；
（II）根据下列表格中的数据，比较两种模型的相关指数
，并选择拟合精度更高、更可靠的模型，预测投资金额为20万元时的年利润增量（结果保留两位小数）.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 102.28 | 36.19 |
附：若随机变量
，则
，
；样本
的最小乘估计公式为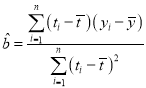
，
；
相关指数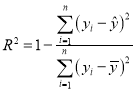
.
参考数据：
，
，
，
.
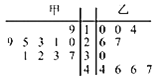
【题目】某校为了解学生对消防安全知识的掌握情况，开展了网上消防安全知识有奖竞赛活动，并对参加活动的男生、女生各随机抽取20人，统计答题成绩，分别制成如下频率分布直方图和茎叶图：
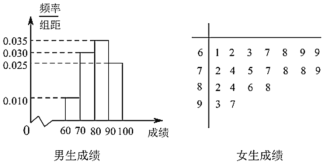
（1）把成绩在80分以上（含80分）的同学称为“安全通”.根据以上数据，完成以下
列联表，并判断是否有95%的把握认为是否是“安全通”与性别有关
男生 | 女生 | 合计 | |
安全通 | |||
非安全通 | |||
合计 |
（2）以样本的频率估计总体的概率，现从该校随机抽取2男2女，设其中“安全通”的人数为
，求的分布列与数学期望.
附：参考公式
，其中
.
参考数据：
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
