题目内容
函数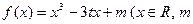 和
和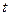 为实常数)是奇函数,设
为实常数)是奇函数,设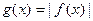 在
在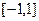 上的最大值为
上的最大值为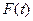 . ⑴求
. ⑴求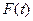 的表达式; ⑵求
的表达式; ⑵求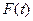 的最小值.
的最小值.
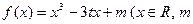 和
和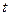 为实常数)是奇函数,设
为实常数)是奇函数,设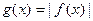 在
在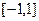 上的最大值为
上的最大值为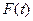 . ⑴求
. ⑴求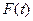 的表达式; ⑵求
的表达式; ⑵求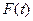 的最小值.
的最小值.(1)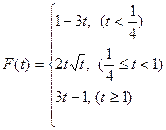 .
.
(2)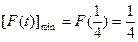 .
.
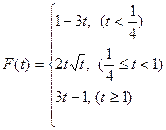 .
.(2)
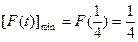 .
.(1)由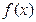 是奇函数知
是奇函数知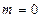 ,所以
,所以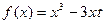 ,
,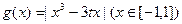 是偶函数,所以,只要求出
是偶函数,所以,只要求出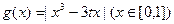 的最大值即可.
的最大值即可.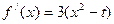 …(2分)
…(2分)
①当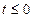 时,
时,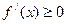 ,
,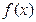 在
在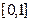 上为增函数,
上为增函数,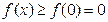 ,∴
,∴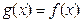
故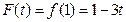 .
.
②当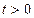 时,
时,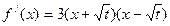 , 由
, 由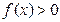 得
得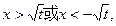
所以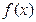 在
在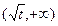 上为增函数,在
上为增函数,在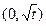 上为减函数,
上为减函数,
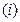 当
当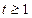 时,
时,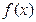 在
在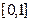 上为减函数,
上为减函数,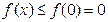 ,∴
,∴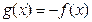
故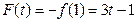 .
.
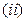 当
当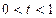 时,
时, 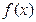 在
在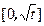 上为减函数,在
上为减函数,在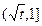 上为增函数,
上为增函数,
当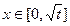 时,
时,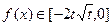 ,当
,当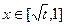 时,
时,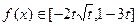 .
.
若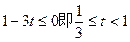 时,
时,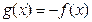 ,∴
,∴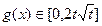 ,∴
,∴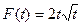 ,
,
若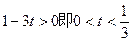 时,∵
时,∵ 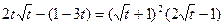
∴当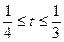 时,
时,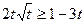 >0,
>0,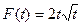 ,当
,当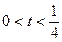 时,
时,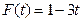 .
.
综上知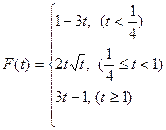 .
.
(2)由(1)知,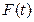 在
在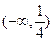 上为减函数,在
上为减函数,在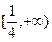 上为增函数,
上为增函数,
∴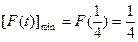 .
.
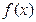 是奇函数知
是奇函数知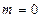 ,所以
,所以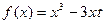 ,
,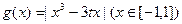 是偶函数,所以,只要求出
是偶函数,所以,只要求出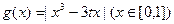 的最大值即可.
的最大值即可.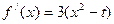 …(2分)
…(2分)①当
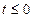 时,
时,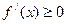 ,
,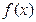 在
在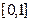 上为增函数,
上为增函数,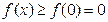 ,∴
,∴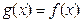
故
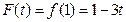 .
. ②当
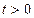 时,
时,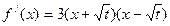 , 由
, 由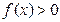 得
得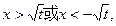
所以
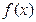 在
在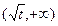 上为增函数,在
上为增函数,在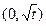 上为减函数,
上为减函数, 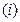 当
当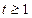 时,
时,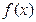 在
在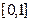 上为减函数,
上为减函数,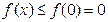 ,∴
,∴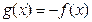
故
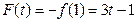 .
.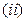 当
当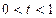 时,
时, 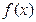 在
在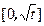 上为减函数,在
上为减函数,在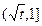 上为增函数,
上为增函数,当
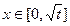 时,
时,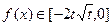 ,当
,当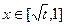 时,
时,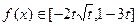 .
.若
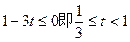 时,
时,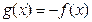 ,∴
,∴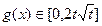 ,∴
,∴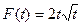 ,
,若
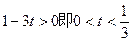 时,∵
时,∵ 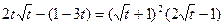
∴当
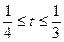 时,
时,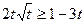 >0,
>0,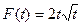 ,当
,当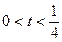 时,
时,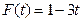 .
.综上知
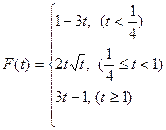 .
.(2)由(1)知,
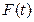 在
在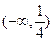 上为减函数,在
上为减函数,在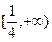 上为增函数,
上为增函数,∴
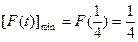 .
.
练习册系列答案
相关题目
 =(1,1),设f(x)=
=(1,1),设f(x)=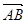 ·
·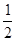 x
x ≤f(x
≤f(x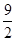 m-3都恒成立,求实数m的取值范围.
m-3都恒成立,求实数m的取值范围.
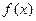 的定义域;
的定义域;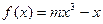 的图象上以N(1,n)为切点的切线倾斜角为
的图象上以N(1,n)为切点的切线倾斜角为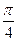 .
.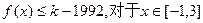 恒成立?若存在,求出最小的正整数k,否则请说明理由.
恒成立?若存在,求出最小的正整数k,否则请说明理由.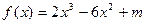 (m为常数)在
(m为常数)在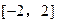 上有最大值3,那么此函数在
上有最大值3,那么此函数在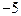
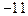
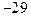
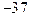
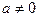 ,函数
,函数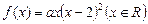 .
.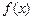 有极大值32,求实数
有极大值32,求实数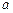 的值;(Ⅱ)若对
的值;(Ⅱ)若对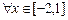 ,不等式
,不等式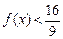 恒成立,求实数
恒成立,求实数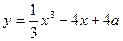 的极大值是
的极大值是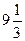 ,则常数
,则常数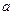 的值是( )
的值是( )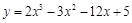 在区间[0,3]上的最大值与最小值分别是( )
在区间[0,3]上的最大值与最小值分别是( )