题目内容
(本小题满分12分)已知A(1,f′(1))是函数y=f(x)的导函数图像上的一点,点B的坐标为(x,㏑(x+1)),向量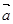 =(1,1),设f(x)=
=(1,1),设f(x)=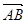 ·
·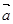
(1)求函数y=f(x)的表达式;
(2)若x∈[-1,1]时,不等式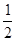 x
x ≤f(x
≤f(x )+m
)+m -
-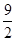 m-3都恒成立,求实数m的取值范围.
m-3都恒成立,求实数m的取值范围.
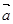 =(1,1),设f(x)=
=(1,1),设f(x)=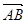 ·
·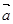
(1)求函数y=f(x)的表达式;
(2)若x∈[-1,1]时,不等式
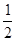 x
x ≤f(x
≤f(x )+m
)+m -
-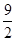 m-3都恒成立,求实数m的取值范围.
m-3都恒成立,求实数m的取值范围.(1)f(x)=ln(x+1)+x-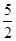
(2)m≤-1或m≥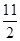 .
.
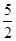
(2)m≤-1或m≥
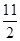 .
.(1)f(x)=ln(x+1)+x-f′(1)-1
则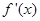 =
=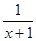 +1,∴f′(1)=
+1,∴f′(1)=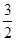 ,∴f(x)=ln(x+1)+x-
,∴f(x)=ln(x+1)+x-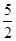
(2)原不等式可化为ln(x +1)+
+1)+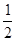 x
x ≥-m
≥-m +
+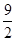 m+
m+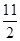
函数y=ln(x +1)+
+1)+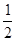 x
x 在x∈[-1,1]上偶函数且在x∈[0,1]是增函数
在x∈[-1,1]上偶函数且在x∈[0,1]是增函数
所以当x=0时函数y=ln(x +1)+
+1)+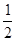 x
x 有最小值0
有最小值0
则只需-m +
+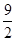 m+
m+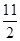 ≤0,解得m≤-1或m≥
≤0,解得m≤-1或m≥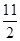 .
.
则
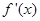 =
=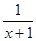 +1,∴f′(1)=
+1,∴f′(1)=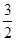 ,∴f(x)=ln(x+1)+x-
,∴f(x)=ln(x+1)+x-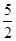
(2)原不等式可化为ln(x
 +1)+
+1)+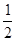 x
x ≥-m
≥-m +
+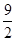 m+
m+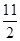
函数y=ln(x
 +1)+
+1)+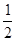 x
x 在x∈[-1,1]上偶函数且在x∈[0,1]是增函数
在x∈[-1,1]上偶函数且在x∈[0,1]是增函数所以当x=0时函数y=ln(x
 +1)+
+1)+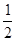 x
x 有最小值0
有最小值0则只需-m
 +
+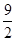 m+
m+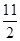 ≤0,解得m≤-1或m≥
≤0,解得m≤-1或m≥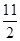 .
.
练习册系列答案
相关题目
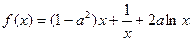 .
.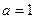 时,求
时,求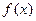 的最小值;
的最小值; 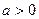 时,求
时,求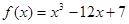 在
在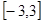 上的最大值与最小值的差是
上的最大值与最小值的差是



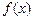 的定义域为
的定义域为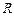 ,导函数
,导函数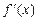 的图像如图所示,给出函数
的图像如图所示,给出函数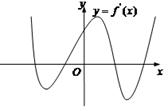
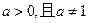 函数
函数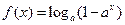 。
。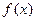 的定义域,并判断
的定义域,并判断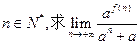 ;
;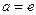 (
(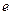 为自然对数的底数)时,设
为自然对数的底数)时,设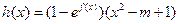 ,若函数
,若函数 的极值存在,求实数
的极值存在,求实数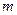 的取值范围以及函数
的取值范围以及函数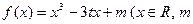 和
和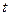 为实常数)是奇函数,设
为实常数)是奇函数,设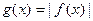 在
在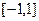 上的最大值为
上的最大值为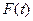 . ⑴求
. ⑴求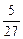
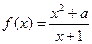 在
在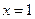 处取得极值,则实数
处取得极值,则实数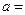 ▲ .
▲ .