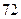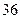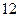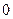题目内容
把8分成两个正整数的和，其一个的立方与另一个的平方和最小，则这两个正整数分别为____________.
2、6
本题考查利用求导的方法求比较复杂函数的最值.关键是设变量，构造目标函数.注意变量的取值范围.
设一个数为x，则另一个数为(8－x).
由条件可设y=x3＋(8－x)2(0＜x＜8,x∈N*)，所以y′=3x2＋2x－16.
令y′=3x2＋2x－16=0,即(x－2)(3x＋8)=0,得x=2.∴8－x=6.
设一个数为x，则另一个数为(8－x).
由条件可设y=x3＋(8－x)2(0＜x＜8,x∈N*)，所以y′=3x2＋2x－16.
令y′=3x2＋2x－16=0,即(x－2)(3x＋8)=0,得x=2.∴8－x=6.
练习册系列答案
阅读快车系列答案
相关题目
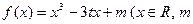和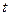
为实常数)是奇函数，设
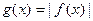在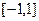
上的最大值为
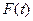. ⑴求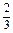
时，y=f(x）有极值.
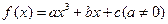为奇函数，导函数
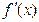的最小值为-12，函数
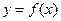的图象在点P
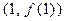处的切线与直线
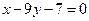垂直.(1)求a，b，c的值；(2)求
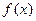的各个单调区间，并求
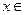[-1, 3]时的最大值和最小值.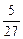
，
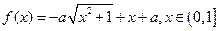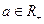，（1）若
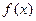在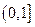
上是增函数，求
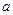的取值范围；（2）求
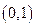上的最大值。
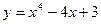在区间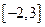
上的最小值为（ ）
