题目内容
7.在平面直角坐标系中,若不等式组$\left\{\begin{array}{l}x+y-2≤0\\ x-y+2≥0\\ y≥t\end{array}\right.$表示的平面区域的面积为1,则实数t的值为( )| A. | 0 | B. | 1 | C. | 3 | D. | -1 |
分析 利用二元一次不等式组的定义作出对应的图象,找出对应的平面区域,利用面积是9,可以求出a的数值.
解答 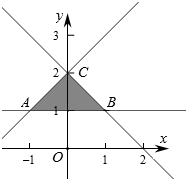 解:作出不等式组对应的平面区域,则t<2,
解:作出不等式组对应的平面区域,则t<2,
由$\left\{\begin{array}{l}{x+y-2=0}\\{y=t}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2-t}\\{y=t}\end{array}\right.$,即B(2-t,t),
由$\left\{\begin{array}{l}{x-y+2=0}\\{y=t}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=t-2}\\{y=t}\end{array}\right.$,即A(t-2,t),
则|AB|=2-t-(t-2)=2(2-t),
C到直线AB的距离d=2-t,
则△的面积S=$\frac{1}{2}×$2(2-t)(2-t)=1,
即(2-t)2=1,
即2-t=1,解得t=1,
故选:B
点评 本题主要考查三角形面积的计算,根据二元一次不等式组表示平面区域作出对应的图象是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.一个几何体的三视图如图所示,则该几何体的表面积为( )


| A. | $\frac{2π}{3}$ | B. | π | C. | 2π | D. | 3π |
15.若直线y=2x-b在x轴上的截距为1,则b=( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
2.已知i为虚数单位,复数z1=a+2i,z2=2-i,且|z1|=|z2|,则实数a的值为( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | ±1或0 |
19.“x<2”是“x(x-1)<0”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
8.已知集合M={2,3,4},N={0,2,3,5},则M∪N中元素的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |