题目内容
12.已知等比数列{an}满足:a2=4,公比q=2,数列{bn}的前n项和为Sn,且Sn=$\frac{4}{3}$bn-$\frac{2}{3}$an+$\frac{2}{3}$(n∈N*).(1)求数列{an}和数列{bn}的通项an和bn;
(2)设Pn=$\frac{a_n}{S_n}(n∈{N^*})$,证明:p1+p2+p3+…+pn<$\frac{3}{2}$.
分析 (1)根据a2=4,公比q=2,确定出等比数列{an}的通项,把{an}通项代入已知等式表示出Sn,由n≥2时,bn=Sn-Sn-1,确定出数列{bn}的通项即可;
(2)把an与Sn代入已知等式变形,整理后利用不等式的放缩即可得证.
解答 解:(1)由a2=4,公比q=2,得,an=a2•2n-2=2n,
代入Sn=$\frac{4}{3}$bn-$\frac{2}{3}$an+$\frac{2}{3}$得:Sn=$\frac{4}{3}$bn-$\frac{2}{3}$(2n-1),
则当n≥2时,bn=Sn-Sn-1=$\frac{4}{3}$bn-$\frac{2}{3}$(2n-1)-$\frac{4}{3}$bn-1+$\frac{2}{3}$(2n-1-1),
整理得:bn+2n=4(bn-1+2n-1),
∵b1=S1=$\frac{4}{3}$b2-$\frac{2}{3}$,∴b1=2,
∴数列{bn+2n}是首项为b1+2=4,公比为4的等比数列,
∴bn+2n=4×4n-1=4n,
∴bn=4n-2n;
(2)由bn=4n-2n,得Sn=$\frac{4}{3}$bn-$\frac{2}{3}$(2n-1)=$\frac{4}{3}$(4n-2n)-$\frac{2}{3}$(2n-1)=$\frac{2}{3}$(2n+1-1)(2n-1),
∴Pn=$\frac{{a}_{n}}{{S}_{n}}$=$\frac{{2}^{n}}{\frac{2}{3}({2}^{n+1}-1)({2}^{n}-1)}$=$\frac{3}{2}$($\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$),
∴$\sum_{i=1}^{n}$pi=p1+p2+p3+…+pn=$\frac{3}{2}$[(1-$\frac{1}{{2}^{2}-1}$)+($\frac{1}{{2}^{2}-1}$-$\frac{1}{{2}^{3}-1}$)+…+($\frac{1}{{2}^{n}-1}$-$\frac{1}{{2}^{n+1}-1}$)]=$\frac{3}{2}$(1-$\frac{1}{{2}^{n+1}-1}$)<$\frac{3}{2}$.
点评 此题考查了数列的求和,等比数列的性质,以及数列的递推式,熟练掌握等比数列的性质是解本题的关键.

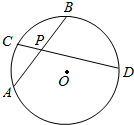 如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )
如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )| A. | 7 | B. | $\sqrt{39}$ | C. | $\sqrt{7}$ | D. | 8 |
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
| A. | 0 | B. | 1 | C. | 3 | D. | -1 |
| A. | { 0,2,3,6 } | B. | { 0,3,6 } | C. | { 1,2,5,8 } | D. | ∅ |