题目内容
17.复数z的共轭复数记为$\overline{z}$,复数z、$\overline{z}$分别对应点Z、$\overline{Z}$.设A是一些复数对应的点组成的集合,若对任意的Z∈A,都有$\overline{Z}$∈A,就称A为“共轭点集”.给出下列点集:①{(x,y)|x2+(y-1)2≤1}; ②{(x,y)|$\left\{\begin{array}{l}{y>2x-4}\\{y<-2x+4}\\{x>0}\end{array}\right.$}; ③{(x,y)|$\frac{{x}^{2}}{2}$-y2=1};
④{(x,y)|y=2x}.其中是“共轭点集”的有②③.
分析 利用已知条件然后判断选项图形的对称性即可.
解答 解:复数z的共轭复数记为$\overline{z}$,复数z、$\overline{z}$分别对应点Z、$\overline{Z}$.设A是一些复数对应的点组成的集合,若对任意的Z∈A,都有$\overline{Z}$∈A,就称A为“共轭点集”.
可知满足性质:复数z、$\overline{z}$分别对应点Z、$\overline{Z}$.对称点关于y轴对称,图形关于x轴对称.
①{(x,y)|x2+(y-1)2≤1}表示的图形不关于x轴对称;所以不是“共轭点集”.
②{(x,y)|$\left\{\begin{array}{l}{y>2x-4}\\{y<-2x+4}\\{x>0}\end{array}\right.$}的图象关于x轴对称; 是“共轭点集”
③{(x,y)|$\frac{{x}^{2}}{2}$-y2=1}的图形关于x轴对称;是“共轭点集”
④{(x,y)|y=2x}的图象关于x轴对称.不是“共轭点集”
故答案为:②③.
点评 本题考查复数的几何意义,图形的对称性,考查分析问题解决问题的能力.

练习册系列答案
相关题目
2.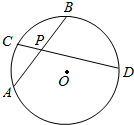 如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )
如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )
 如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )
如图,圆O内的两条弦AB、CD相交于P,PA=PB=4,PD=4PC.若O到AB的距离为4,则O到CD的距离为( )| A. | 7 | B. | $\sqrt{39}$ | C. | $\sqrt{7}$ | D. | 8 |
6.一个商场经销某种商品,根据以往资料统计,每位顾客采用的分期付款次数ξ的分布列为:
商场经销一件该商品,采用1期付款,其利润为200元;采用2期或3期付款,其利润为250元;采用4期或5期付款,其利润为300元.η表示经销一件该商品的利润.
(1)求购买该商品的3位顾客中,恰有2位采用1期付款的概率;
(2)求η的分布列及期望E(η).
| ξ | 1 | 2 | 3 | 4 | 5 |
| P | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
(1)求购买该商品的3位顾客中,恰有2位采用1期付款的概率;
(2)求η的分布列及期望E(η).
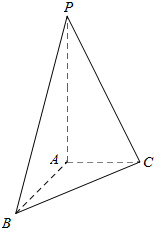 如图,在三棱锥P-ABC中,PA丄平面ABC,AC丄AB,PA=AB=2,AC=1.
如图,在三棱锥P-ABC中,PA丄平面ABC,AC丄AB,PA=AB=2,AC=1.