题目内容
20.设a∈R,则“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的充分性不必要条件.分析 根据直线平行的等价条件以及充分条件和必要条件的定义进行判断.
解答 解:若a=1,则两直线方程为x+2y-1=0,和x+2y+4=0,此时两直线平行,
若两直线平行,
则当a=0时,两直线方程为2y-1=0,和x+y+4=0,此时两直线相交,不平行不满足条件.
当a≠0时,若两直线方程平行,则满足$\frac{1}{a}=\frac{a+1}{2}≠\frac{4}{-1}$,
即a(a+1)=2,即a2+a-2=0,
解得a=1或a=-2,此时满足条件,
故“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的充分不必要条件,
故答案为:充分不必要.
点评 本题主要考查充分条件和必要条件的判断,根据直线平行的等价条件是解决本题的关键.

练习册系列答案
相关题目
11.二次函数f(x)=ax2+bx+c(a>0)的图象与x轴交点的横坐标为-5和3,则这个二次函数的单调减区间为( )
| A. | (-∞,-1] | B. | [2,+∞) | C. | (-∞,2] | D. | [-1,+∞) |
5.阅读如图所示的程序框图,运行相应的程序,当输入x的值为-25时,输出x的值为( )
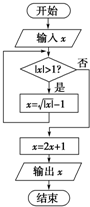

| A. | 9 | B. | 3 | C. | 1 | D. | -1 |
9.若实数a,b,c,d满足(b+2a2-6lna)2+|2c-d+6|=0,(a-c)2+(b-d)2的最小值为m,则函数f(x)=ex+$\frac{1}{5}$mx-3零点所在的区间为( )
| A. | $({-\frac{1}{4},0})$ | B. | $({0,\frac{1}{4}})$ | C. | $({\frac{1}{4},\frac{1}{2}})$ | D. | $({\frac{1}{2},1})$ |
 三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{{2\sqrt{3}}}{3}$.
三棱锥的三视图如图所示,则该三棱锥的体积为$\frac{{2\sqrt{3}}}{3}$.