题目内容
9.若实数a,b,c,d满足(b+2a2-6lna)2+|2c-d+6|=0,(a-c)2+(b-d)2的最小值为m,则函数f(x)=ex+$\frac{1}{5}$mx-3零点所在的区间为( )| A. | $({-\frac{1}{4},0})$ | B. | $({0,\frac{1}{4}})$ | C. | $({\frac{1}{4},\frac{1}{2}})$ | D. | $({\frac{1}{2},1})$ |
分析 由题意可得b=6lna-2a2,d=2c+6;而(a-c)2+(b-d)2的几何意义是点(a,b)与点(c,d)的距离的平方;从而化为求函数y=6lnx-2x2上的点到直线y=2x+6的距离的平方的最小值,从而由导数求切点,从而求出m,再由函数零点的判定定理求解即可.
解答 解:∵(b+2a2-6lna)2+|2c-d+6|=0,
∴b+2a2-6lna=0,2c-d+6=0;
即b=6lna-2a2,d=2c+6;
而(a-c)2+(b-d)2的几何意义是点(a,b)与点(c,d)的距离的平方;
故m是函数y=6lnx-2x2上的点到直线y=2x+6的距离的平方的最小值;
令y′=$\frac{6}{x}$-4x=2得,x=1;
故切点坐标为(1,-2);
故m=$(\frac{|2+6-(-2)|}{\sqrt{{2}^{2}+1}})^{2}$=20;
故函数f(x)=ex+4x-3;
而f($\frac{1}{4}$)=$\root{4}{e}$+1-3=$\root{4}{e}$-2<0,
f($\frac{1}{2}$)=$\sqrt{e}$+2-3=$\sqrt{e}$-1>0;
故f($\frac{1}{4}$)f($\frac{1}{2}$)<0;
故函数f(x)=ex+$\frac{1}{5}$mx-3零点所在的区间为($\frac{1}{4}$,$\frac{1}{2}$);
故选:C.
点评 本题考查了导数的几何意义的应用及函数的应用,同时考查了函数零点的判定定理的应用,属于中档题.

练习册系列答案
相关题目
19.设函数f(x)=$\sqrt{3}+\frac{sinx}{1+cosx}$的所有正的零点从小到大依次为x1,x2,x3,…,设α=x1+x2+x3+…+x2015,则sinα的值是( )
| A. | 0 | B. | -$\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
14.若实数a,b,c,d满足(b+2a2-6lna)2+|2c-d+6|=0,则(a-c)2+(b-d)2的最小值为( )
| A. | 5 | B. | $2\sqrt{5}$ | C. | 20 | D. | 4$\sqrt{5}$ |
18.甲、乙两人参加某单位招聘面试测试,每次测试从试题库随机用一套试题,他们参加的5项测试成绩记录如下:
(1)用茎叶图表示甲、乙这5项测试成绩;
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)现要根据测试成绩选择一人到该单位,从统计学的角度考虑,你认为选择哪位合适,说明理由.
| 甲 | 82 | 82 | 79 | 95 | 87 |
| 乙 | 95 | 75 | 80 | 90 | 85 |
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)现要根据测试成绩选择一人到该单位,从统计学的角度考虑,你认为选择哪位合适,说明理由.
19.如图三角形OAB为用斜二测画法所画的直观图,其原来平面图形的面积是( )
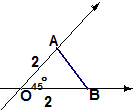

| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 8 |