Question

15．三棱锥的三视图如图所示，则该三棱锥的体积为$\frac{{2\sqrt{3}}}{3}$．

Answer 1

分析 根据几何体的三视图，得出该几何体底面为直角三角形的三棱锥，且侧棱垂直于底面，求出它的体积即可．

解答 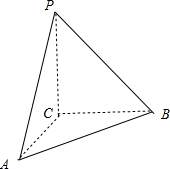解：根据几何体的三视图，得；
该几何体是如图所示的三棱锥P-ABC，
且PC⊥底面ABC，AC⊥BC；
PC=BC=2，AC=$\sqrt{3}$；
所以，该三棱锥的体积为
V=$\frac{1}{3}$×$\frac{1}{2}$×2×$\sqrt{3}$×2=$\frac{2}{3}$$\sqrt{3}$．
故答案为：$\frac{2\sqrt{3}}{3}$．

点评 本题考查了空间几何体的三视图的应用问题，也考查了空间想象能力与计算能力，是基础题目．