题目内容
【题目】已知椭圆C：
1（a＞b＞0）的离心率e
，且点P（
，1）在椭圆C上.
（1）求椭圆C的方程；
（2）若椭圆C的左焦点为F，右顶点为A，点M（s，t）（t＞0）是椭圆C上的动点，直线AM与y轴交于点D，点E是y轴上一点，EF⊥DF，EA与椭圆C交于点G，若△AMG的面积为2，求直线AM的方程.
【答案】（1）
（2）x
y﹣2＝0
【解析】
（1）利用离心率和椭圆经过的点建立方程组，可以求解方程；
（2）设出直线方程，联立方程组，结合三角形的面积为2
可得直线斜率，从而可得方程.
（1）由题意得e
，
，a2＝b2+c2，解得：a2＝4，b2＝2，
所以椭圆的方程：
.
（2）由（1）得左焦点F（
，0），A（2，0），设直线AM：y＝k（x﹣2），由题意得D（0，﹣2k），∴kDF
k，
∵EF⊥DF，∴kEF
，∴直线EF的方程：x
，
令x＝0，则y
，所以点E（0，
），所以kEA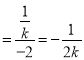
，
所以直线EA：x＝﹣2ky+2，联立与椭圆的方程整理得：∴y
，x
，所以点G（
，
）；
联立直线AM与椭圆的方程整理得：（1+2k2）x2﹣8k2x+8k2﹣4＝0，解得：x1＝2，x2
，∴y2
，所以点M（
，
），
所以点M，G关于原点对称，即直线MG过原点，
∴S△AMG
2|yM|
，由题意得：
2，解得：k
，
由点M（s，t）（t＞0）得，k
，所以直线AM为：y（x﹣2），
即直线AM：x
y﹣2＝0.
练习册系列答案
阅读快车系列答案
相关题目
