题目内容
【题目】如图所示的多面体ABCDEF满足:正方形ABCD与正三角形FBC所在的两个平面互相垂直,FB∥AE且FB=2EA.
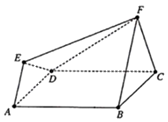
(1)证明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)先证明AB⊥平面BCF,然后可得平面EFD⊥平面ABFE;
(2)建立空间直角坐标系,求解平面的法向量,然后利用向量的夹角公式可求.
(1)由题可得,因为ABCD是正方形且三角形FBC是正三角形,所以BC∥AD,BC=AD,FB=BC且∠FBC=60°,
又因为EA∥FB,2EA=FB,所以∠EAD=60°,在三角形EAD中,根据余弦定理可得:ED⊥AE.
因为平面ABCD⊥平面FBC,AB⊥BC,平面ABCD∩平面FBC=BC,且AB平面ABCD,所以AB⊥平面BCF,
因为BC∥AD, E A∥FB,FB∩BC=B,且FB、BC平面FCB,EA、AD平面EAD,所以平面EAD∥平面FBC,所以AB⊥平面EAD,
又因为ED平面EAD,所以AB⊥ED,
综上:ED⊥AE,ED⊥AB,EA∩AB=A且EA、AB平面ABFE,所以DE⊥平面ABFE,
又DE平面DEF,所以平面EFD⊥平面ABFE.
(2)如图,分别取BC和AD的中点O,G,连接OF,OG,
因为BO=OC且三角形FBC为正三角形,所以FO⊥BC,
因为AG=GD,BO=OC,所以OG∥AB,
由(1)可得,AB⊥平面FBC,则OG⊥平面FBC,
故OF、OB、OG两两垂直,分别以OB、OG、OF所在直线为x,y,z轴建立如图所示的空间直角坐标系,

不妨设BC=4,则![]() ,
,![]()
设平面DEF的法向量为![]() ,平面DCF的法向量为
,平面DCF的法向量为![]() ,
,
则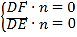
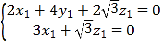
![]() ,
,
则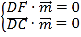
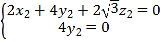
![]() ,
,
所以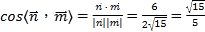
又二面角E﹣FD﹣C是钝二面角,所以二面角E﹣FD﹣C的余弦值为![]() .
.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案