题目内容
【题目】已知函数f(x)=![]() x3(a>0且a≠1).
x3(a>0且a≠1).
(1)求函数f(x)的定义域;
(2)讨论函数f(x)的奇偶性;
(3)求a的取值范围,使f(x)>0在定义域上恒成立.
【答案】(1){x|x∈R,且x≠0}(2)偶函数(3)a>1.
【解析】
(1)由于ax-1≠0,则ax≠1,所以x≠0,
所以函数f(x)的定义域为{x|x∈R,且x≠0}.
(2)对于定义域内任意的x,有
f(-x)=![]() (-x)3=-
(-x)3=-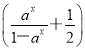 x3=-
x3=-![]() x3=
x3=![]() x3=f(x)所以f(x)是偶函数.
x3=f(x)所以f(x)是偶函数.
(3)①当a>1时,对x>0,
所以ax>1,即ax-1>0,所以![]() +
+![]() >0.
>0.
又x>0时,x3>0,所以x3![]() >0,
>0,
即当x>0时,f(x)>0.
由(2)知,f(x)是偶函数,即f(-x)=f(x),
则当x<0时,-x>0,有f(-x)=f(x)>0成立.
综上可知,当a>1时,f(x)>0在定义域上恒成立.
②当0<a<1时,f(x)=![]() ,
,
当x>0时,0<ax<1,此时f(x)<0,不满足题意;
当x<0时,-x>0,有f(-x)=f(x)<0,也不满足题意.
综上可知,所求a的取值范围是a>1

练习册系列答案
相关题目
【题目】通过市场调查,得到某种产品的资金投入x(单位:万元)与获得的利润y(单位:万元)的数据,如表所示:
资金投入x | 2 | 3 | 4 | 5 | 6 |
利润y | 2 | 3 | 5 | 6 | 9 |
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() ;
;
(3)现投入资金10万元,求获得利润的估计值为多少万元?
参考公式:
