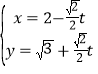题目内容
【题目】已知椭圆C:![]() (
(![]() ),其中离心率
),其中离心率![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 为椭圆的左右焦点,若
为椭圆的左右焦点,若![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 的上顶点,若
的上顶点,若![]() ,试问直线
,试问直线![]() 是否经过定点,若经过定点,求出定点坐标,否则说明理由.
是否经过定点,若经过定点,求出定点坐标,否则说明理由.
【答案】(1)![]() ; (2)直线
; (2)直线![]() 恒过定点
恒过定点![]()
【解析】
(1)直接由离心率及面积的最大值和![]() 之间的关系求出椭圆的标准方程;
之间的关系求出椭圆的标准方程;
(2)由(1)知![]() 点坐标,假设直线,联立与椭圆的方程,得出两根之和两根之积,由直线垂直得数量积为零求出过的定点.
点坐标,假设直线,联立与椭圆的方程,得出两根之和两根之积,由直线垂直得数量积为零求出过的定点.
(1)由题意得:e![]() ,
,![]() ,
,![]() ,
,
解得:![]() ,所以椭圆的C的标准方程:
,所以椭圆的C的标准方程:![]() ;
;
(2)由(1)得,![]() ,显然直线
,显然直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程:
的方程:![]() ,
,
设![]() ,
,
联立方程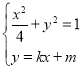 与椭圆的方程整理得:
与椭圆的方程整理得:![]() ,
,
![]() ,即
,即![]() ,
,
所以![]() ,
, 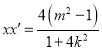 ,
,
所以![]() ,
, ![]() ,
,
因为![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,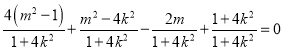 ,
,
∴![]() ,解得:
,解得:![]() ,
,
当![]() 时,直线
时,直线![]() 过B点不符合条件,舍去,
过B点不符合条件,舍去,
当![]() 时,符合
时,符合![]() ,
,
所以直线![]() 恒过定点
恒过定点![]() .
.

【题目】2018年非洲猪瘟在东北三省出现,为了进行防控,某地生物医药公司派出技术人员对当地甲乙两个养殖场提供技术服务,方案和收费标准如下:
方案一,公司每天收取养殖场技术服务费40元,对于需要用药的每头猪收取药费2元,不需要用药的不收费;
方案二,公司每天收取养殖场技术服务费120元,若需要用药的猪不超过45头,不另外收费,若需要用药的猪超过45头,超过部分每天收取药费8元.
(1)设日收费为![]() (单位:元),每天需要用药的猪的数量为
(单位:元),每天需要用药的猪的数量为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)若该医药公司从10月1日起对甲养殖场提供技术服务,10月31日该养殖场对其中一个猪舍9月份和10月份猪的发病数量进行了统计,得到如下![]() 列联表.
列联表.
9月份 | 10月份 | 合计 | |
未发病 | 40 | 85 | 125 |
发病 | 65 | 20 | 85 |
合计 | 105 | 105 | 210 |
根据以上列联表,判断是否有![]() 的把握认为猪未发病与医药公司提供技术服务有关.
的把握认为猪未发病与医药公司提供技术服务有关.
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
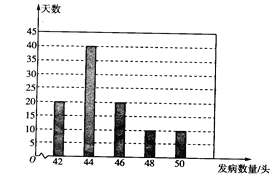
(3)当地的丙养殖场对过去100天猪的发病情况进行了统计,得到如上图所示的条形统计图.依据该统计数据,从节约养殖成本的角度去考虑,若丙养殖场计划结合以往经验从两个方案中选择一个,那么选择哪个方案更合适,并说明理由.
【题目】2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专章规定.草案提出,国家推行生活垃圾分类制度.为了了解人民群众对垃圾分类的认识,某市环保部门对该市市民进行了一次垃圾分类网络知识问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如表所示:
得分 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,市环保部门为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() “的可以获赠2次随机话费,得分低于
“的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;②若
;②若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,