题目内容
设数列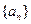 ,
,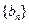 满足
满足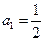 ,
,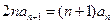 ,且
,且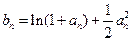 ,
,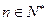
(1)求数列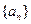 的通项公式;(2)对一切
的通项公式;(2)对一切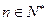 ,证明
,证明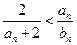 成立;
成立;
(3)记数列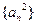 ,
,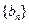 的前
的前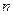 项和分别是
项和分别是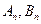 ,证明
,证明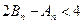 。
。
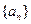 ,
,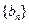 满足
满足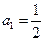 ,
,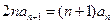 ,且
,且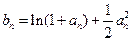 ,
,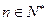
(1)求数列
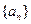 的通项公式;(2)对一切
的通项公式;(2)对一切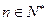 ,证明
,证明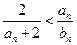 成立;
成立;(3)记数列
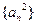 ,
,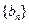 的前
的前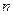 项和分别是
项和分别是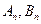 ,证明
,证明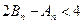 。
。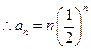
解:(1)由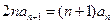 ,得
,得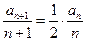 ,即数列{
,即数列{ }是以
}是以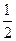 为首项,以
为首项,以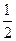 为公比的等比数列,
为公比的等比数列,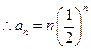 ……..3分
……..3分
(2)因为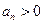 ,
, 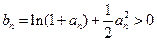 ,
,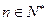 ,所以要证明
,所以要证明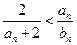 ,只需证明
,只需证明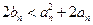 ,即证
,即证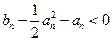 ,即证明
,即证明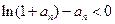 成立,构造函数
成立,构造函数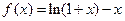 (
(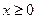 ),
),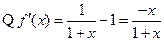 ,当
,当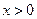 时
时 ,即
,即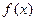 在(
在(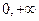 )上单调递减,故
)上单调递减,故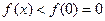 ,
,
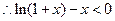 ,即
,即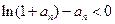 ,
,
对一切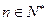 都成立,所以
都成立,所以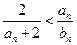 。………7分
。………7分
(3)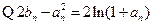 ,由(2)可知,
,由(2)可知,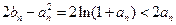 ,
,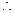
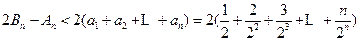
利用错位相减求得: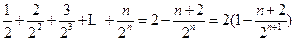
因为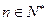 ,所以
,所以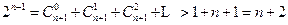
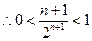 ,所以
,所以 。…..12分
。…..12分
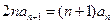 ,得
,得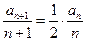 ,即数列{
,即数列{ }是以
}是以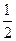 为首项,以
为首项,以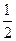 为公比的等比数列,
为公比的等比数列,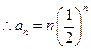 ……..3分
……..3分(2)因为
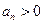 ,
, 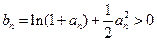 ,
,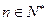 ,所以要证明
,所以要证明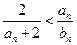 ,只需证明
,只需证明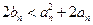 ,即证
,即证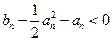 ,即证明
,即证明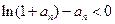 成立,构造函数
成立,构造函数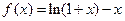 (
(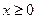 ),
),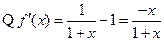 ,当
,当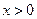 时
时 ,即
,即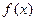 在(
在(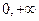 )上单调递减,故
)上单调递减,故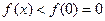 ,
,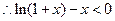 ,即
,即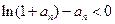 ,
,对一切
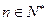 都成立,所以
都成立,所以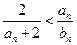 。………7分
。………7分(3)
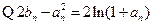 ,由(2)可知,
,由(2)可知,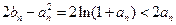 ,
,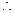
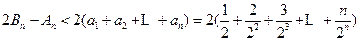
利用错位相减求得:
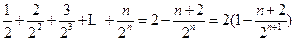
因为
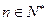 ,所以
,所以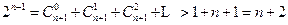
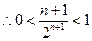 ,所以
,所以 。…..12分
。…..12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
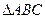 分割成
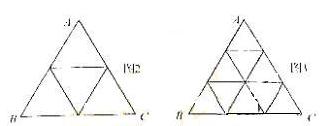
分割成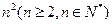 个全等的小正三角形(图2,图3分别给出了n="2," 3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列.若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为
个全等的小正三角形(图2,图3分别给出了n="2," 3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列.若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为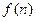 ,则有
,则有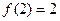 ,
,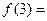 ,… ,
,… ,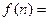 .
.
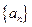 中,
中,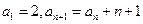 ,则通项
,则通项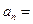 ___________。
___________。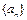 中,
中,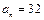 ,
,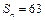 ,
,
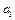 ;
;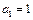 为首项的等比数列,求数列
为首项的等比数列,求数列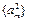 的前m项和
的前m项和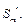
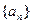 中,
中,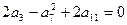 ,数列
,数列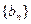 是等比数列,且
是等比数列,且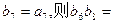 ( )
( )