题目内容
将正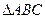 分割成
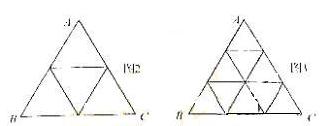
分割成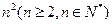 个全等的小正三角形(图2,图3分别给出了n="2," 3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列.若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为
个全等的小正三角形(图2,图3分别给出了n="2," 3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列.若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为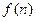 ,则有
,则有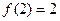 ,
,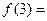 ,… ,
,… ,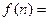 .
.
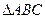 分割成
分割成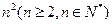 个全等的小正三角形(图2,图3分别给出了n="2," 3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列.若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为
个全等的小正三角形(图2,图3分别给出了n="2," 3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列.若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为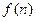 ,则有
,则有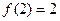 ,
,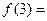 ,… ,
,… ,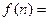 .
.
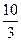 ;
;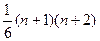
若依题意顶点A ,B ,C处的三个数互不相同且和为1,按等差数列的性质进行计算则显然运算量较大,故常规思维不可取!可偏偏特取A ,B ,C处的数均为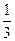 (极限法)来思考:
(极限法)来思考:
则图2中有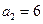 个
个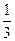 ,得
,得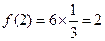 ;故图3中有
;故图3中有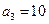 个
个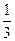 ,得
,得
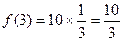 ;易知
;易知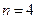 时有
时有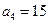 个
个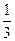 ,
,
探讨数列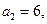
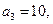
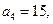
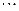
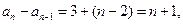
(可参考2006湖南卷:逆序数)由叠加法推知:
 个
个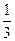 ,
,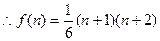 .
.
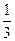 (极限法)来思考:
(极限法)来思考:则图2中有
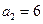 个
个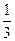 ,得
,得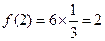 ;故图3中有
;故图3中有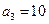 个
个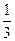 ,得
,得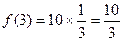 ;易知
;易知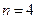 时有
时有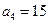 个
个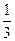 ,
,
探讨数列
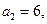
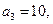
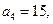
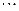
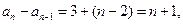
(可参考2006湖南卷:逆序数)由叠加法推知:
 个
个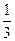 ,
,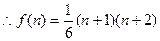 .
.
练习册系列答案
相关题目
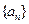 是公方差为
是公方差为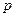 (p>0,an >0)的等方差数列,
(p>0,an >0)的等方差数列,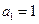 求
求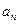 的通项公式;
的通项公式;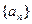 中,前n项和为
中,前n项和为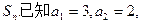
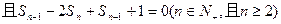
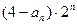 }的前n项和Tn.
}的前n项和Tn.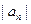 ,
,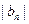 中,a1=2,b1=4,且
中,a1=2,b1=4,且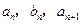 成等差数列,
成等差数列,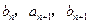 成等比数列(
成等比数列(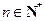 )
)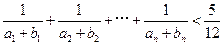 .
. 中,已知
中,已知 则
则 等于
等于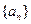 ,
,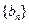 满足
满足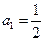 ,
,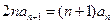 ,且
,且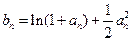 ,
,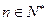
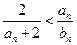 成立;
成立;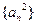 ,
,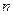 项和分别是
项和分别是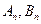 ,证明
,证明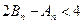 。
。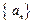 中,
中, ,
, ,则
,则 等于C
等于C