题目内容
13.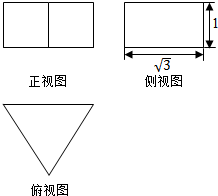 若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )| A. | $\sqrt{3}$ | B. | 6+2$\sqrt{3}$ | C. | 6+$\sqrt{3}$ | D. | $\frac{9\sqrt{3}}{2}$ |
分析 根据正三棱柱的三视图,得出三棱柱的高已经底面三角形的高,求出底面三角形的面积与侧面积即可.
解答 解:根据几何体的三视图,得;
该几何体是底面为正三角形,高为1的正三棱柱;
且底面三角形的高是$\sqrt{3}$;
所以底面三角形的边长是a=$\frac{\sqrt{3}}{si{n60}^{°}}$=2,
所以,该三棱柱的表面积为
S侧面积+S底面积=3×2×1+2×$\frac{1}{2}$×2×$\sqrt{3}$=6+2$\sqrt{3}$.
故选:B.
点评 本题考查了利用几何体的三视图求表面积的应用问题,是基础题目.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
18.100件产品中有5件次品,不放回地抽取两次,每次抽1件,已知第一次抽出的是次品,则第2次抽出正品的概率为( )
| A. | $\frac{19}{20}$ | B. | $\frac{19}{400}$ | C. | $\frac{1}{20}$ | D. | $\frac{95}{99}$ |