题目内容
8.已知锐角α,β满足sinα=$\frac{2\sqrt{5}}{5}$,cosβ=$\frac{\sqrt{10}}{10}$,则α+β=( )| A. | $\frac{π}{4}$ | B. | $\frac{3}{4}$π | C. | $\frac{π}{4}$或$\frac{3}{4}$π | D. | $\frac{π}{2}$ |
分析 由题意和同角三角函数的基本关系可得cosα和sinβ的值,进而可得cos(α+β)的值,结合角的范围可得.
解答 解:锐角α,β满足sinα=$\frac{2\sqrt{5}}{5}$,cosβ=$\frac{\sqrt{10}}{10}$,
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{\sqrt{5}}{5}$,同理sinβ=$\frac{3\sqrt{10}}{10}$,
∴cos(α+β)=cosαcosβ-sinαsinβ=$\frac{\sqrt{5}}{5}×\frac{\sqrt{10}}{10}-\frac{2\sqrt{5}}{5}×\frac{3\sqrt{10}}{10}$=-$\frac{\sqrt{2}}{2}$
由α,β为锐角可得0<α+β<π,
∴α=$\frac{3π}{4}$
故选:B
点评 本题考查两角和与差的三角函数公式,涉及同角三角函数的基本关系,属基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
19.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若$\overrightarrow{PF}$=4$\overrightarrow{FQ}$,则|QF|5.
17.记a=ee,b=ππ,c=eπ,d=πe,则a,b,c,d的大小关系为( )
| A. | a<d<c<b | B. | a<c<d<b | C. | b<a<d<c | D. | b<c<d<a |
18.100件产品中有5件次品,不放回地抽取两次,每次抽1件,已知第一次抽出的是次品,则第2次抽出正品的概率为( )
| A. | $\frac{19}{20}$ | B. | $\frac{19}{400}$ | C. | $\frac{1}{20}$ | D. | $\frac{95}{99}$ |
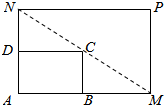 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点.已知AB=3米,AD=2米.设AN=x(单位:米),若x∈[3,4](单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点.已知AB=3米,AD=2米.设AN=x(单位:米),若x∈[3,4](单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积.