题目内容
18.若函数y=Asin(ωx+φ)的图形在y轴右侧的第一个最高点为M(2,3),与x轴在原点右侧的第一个交点为N(6,0),求这个函数的关系式.分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
解答 解:由题意可得函数的周期为$\frac{2π}{ω}$=4(6-2),求得ω=$\frac{π}{8}$,且A=3.
再根据五点法作图可得2×$\frac{π}{8}$+φ=$\frac{π}{2}$,求得φ=$\frac{π}{4}$,∴函数y=3sin($\frac{π}{8}$x+$\frac{π}{4}$).
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
8.已知平面中三点A(-1,-1),B(1,2),C(8,-2),判断三角形ABC的形状( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法判断 |
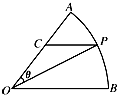 在扇形AOB中,圆心角等于$\frac{π}{3}$,半径为4,在弧AB上有一动点P(不与点AB重合),过点P引平行于OB的直线和OA交于点C,设∠AOP=θ,求三角形POC的面积的最大值及此时θ的值.
在扇形AOB中,圆心角等于$\frac{π}{3}$,半径为4,在弧AB上有一动点P(不与点AB重合),过点P引平行于OB的直线和OA交于点C,设∠AOP=θ,求三角形POC的面积的最大值及此时θ的值.