题目内容
【题目】某电子产品公司前四年的年宣传费x（单位：千万元）与年销售量y（单位：百万部）的数据如下表所示：
x（单位：千万元） | 1 | 2 | 3 | 4 |
y（单位：百万部） | 3 | 5 | 6 | 9 |
可以求y关于x的线性回归方程为 
=1.9x+1．
参考公式：回归方程 = 
x+ 
中斜率和截距的最小二乘法估计公式分别为： = 
， = 
﹣ 
．
（1）该公司下一年准备投入10千万元的宣传费，根据所求得的回归方程预测下一年的销售量m：
（2）根据下表所示五个散点数据，求出y关于x的线性回归方程 = x+ ．
x（单位：千万元） | 1 | 2 | 3 | 4 | 10 |
y（单位：百万部） | 3 | 5 | 6 | 9 | m |
并利用小二乘法的原理说明 = x+ 与 =1.9x+1的关系．
【答案】
（1）解：根据y关于x的线性回归方程为 
=1.9x+1，
计算x=10时， =1.9×10+1=20；
即公司投入10千万元的宣传费，预测下一年的销售量m=20百万部
（2）解：根据下表所示五个散点数据，
计算 
= 
×（1+2+3+4+10）=4，
= ×（3+5+6+9+20）=6.6；
x（单位：千万元） | 1 | 2 | 3 | 4 | 10 |
y（单位：百万部） | 3 | 5 | 6 | 9 | 20 |
∴ 
xiyi=1×3+2×5+3×6+4×9+10×20=267，
=12+22+32+42+102=130，
∴回归系数为 
= 
= 
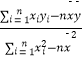=2.7，
= ﹣ 
=6.6﹣2.7×4=﹣4.2，
求出线性回归方程为 =2.7x﹣4.2；
散点图中点的分布从整体上看大致在一条直线附近，
称这两个变量之间具有线性相关关系，这条直线叫做回归直线；
使得样本数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法
【解析】（1）根据线性回归方程计算x=10时 的值即可；（2）根据表中五个散点数据，计算 、 以及回归系数，写出线性回归方程， 解释回归直线与最小二乘法的关系即可．
