题目内容
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的焦点为F1 , F2 , 离心率为
=1(a>b>0)的焦点为F1 , F2 , 离心率为 ![]() ,点P为其上动点,且三角形PF1F2的面积最大值为
,点P为其上动点,且三角形PF1F2的面积最大值为 ![]() ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)若点M,N为C上的两个动点,求常数m,使 ![]() =m时,点O到直线MN的距离为定值,求这个定值.
=m时,点O到直线MN的距离为定值,求这个定值.
【答案】
(1)
解:由题意可知椭圆的离心率e= ![]() =
= ![]() ,则a=2c,
,则a=2c,
当P位于短轴的端点时,△PF1F2的面积最大,即 ![]() ×2c×b=
×2c×b= ![]() ,bc=
,bc= ![]() ,
,
由a2=b2+c2,则a=2,b= ![]() ,c=1,
,c=1,
∴椭圆的标准方程: ![]()
(2)
解:设M(x1,y1)、N(x2,y2), ![]() =x1x2+y1y2=m,
=x1x2+y1y2=m,
当直线MN到斜率存在时,设其方程:y=kx+b,
则点O到直线MN的距离d= ![]() ,
,
则 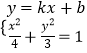 ,整理得:(4k2+3)x2+8kbx+4b2﹣12=0,
,整理得:(4k2+3)x2+8kbx+4b2﹣12=0,
由△>0,整理得:4k2﹣b2+3>0,
由x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
则x1x2+(kx1+b)(kx2+b)=(k2+1)x1x2+kb(x1+x2)+b2=m,
整理得:7× ![]() =12+
=12+ ![]() ,为常数,则m=0,d=
,为常数,则m=0,d= ![]() =
= ![]() ,
,
此时7× ![]() =12,满足△>0,
=12,满足△>0,
当MN⊥x轴时,m=0,整理得kOM=±1,
![]() ,则x2=
,则x2= ![]() ,
,
则d=丨x丨= ![]() ,亦成立,
,亦成立,
综上可知:m=0,d= ![]()
【解析】(1)由题意可知:由椭圆的离心率e= ![]() ,则a=2c,当P位于短轴的端点时,△PF1F2的面积最大,在bc=
,则a=2c,当P位于短轴的端点时,△PF1F2的面积最大,在bc= ![]() 及a2=b2+c2 , 即可求得a和b的值,即可求得椭圆方程;(2)分类讨论,当直线MN的斜率存在时,设其方程,代入椭圆方程,根据点到直线的距离公式,韦达定理及向量数量积的坐标运算,要使7×
及a2=b2+c2 , 即可求得a和b的值,即可求得椭圆方程;(2)分类讨论,当直线MN的斜率存在时,设其方程,代入椭圆方程,根据点到直线的距离公式,韦达定理及向量数量积的坐标运算,要使7× ![]() =12+
=12+ ![]() ,为常数,则m=0,d=
,为常数,则m=0,d= ![]() =
= ![]() ,当直线的斜率不存在时,d=丨x丨=
,当直线的斜率不存在时,d=丨x丨= ![]() ,亦成立.
,亦成立.

【题目】某学校为了解本校学生的身体素质情况,决定在全校的1000名男生和800名女生中按分层抽样的方法抽取45名学生对他们课余参加体育锻炼时间进行问卷调查,将学生课余参加体育锻炼时间的情况分三类:A类(课余参加体育锻炼且平均每周参加体育锻炼的时间超过3小时),B类(课余参加体育锻炼但平均每周参加体育锻炼的时间不超过3小时),C类(课余不参加体育锻炼),调查结果如表:
A类 | B类 | C类 | |
男生 | 18 | x | 3 |
女生 | 10 | 8 | y |
(1)求出表中x、y的值;
(2)根据表格统计数据,完成下面的列联表,并判断是否有90%的把握认为课余参加体育锻炼且平均每周参加体育锻炼的时间超过3小时与性别有关;
男生 | 女生 | 总计 | |
A类 | |||
B类和C类 | |||
总计 |
(3)在抽取的样本中,从课余不参加体育锻炼学生中随机选取三人进一步了解情况,求选取三人中男女都有且男生比女生多的概率. 附:K2= ![]()
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
【题目】某电子产品公司前四年的年宣传费x(单位:千万元)与年销售量y(单位:百万部)的数据如下表所示:
x(单位:千万元) | 1 | 2 | 3 | 4 |
y(单位:百万部) | 3 | 5 | 6 | 9 |
可以求y关于x的线性回归方程为 ![]() =1.9x+1.
=1.9x+1.
参考公式:回归方程 ![]() =
= ![]() x+
x+ ![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
(1)该公司下一年准备投入10千万元的宣传费,根据所求得的回归方程预测下一年的销售量m:
(2)根据下表所示五个散点数据,求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() .
.
x(单位:千万元) | 1 | 2 | 3 | 4 | 10 |
y(单位:百万部) | 3 | 5 | 6 | 9 | m |
并利用小二乘法的原理说明 ![]() =
= ![]() x+
x+ ![]() 与
与 ![]() =1.9x+1的关系.
=1.9x+1的关系.