题目内容
【题目】牛顿法求方程f（x）=0近似根原理如下：求函数y=f（x）在点（xn ， f（xn））处的切线y=f′（xn）（x﹣xn）+f（xn），其与x轴交点横坐标xn+1=xn﹣ 
（n∈N*），则xn+1比xn更靠近f（x）=0的根，现已知f（x）=x2﹣3，求f（x）=0的一个根的程序框图如图所示，则输出的结果为（ ） 
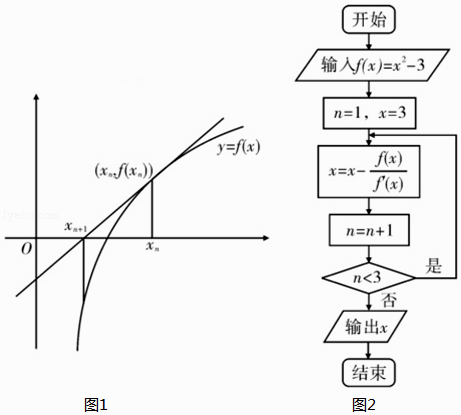
A.2
B.1.75
C.1.732
D.1.73
【答案】B
【解析】解：f（x）=x2﹣3，则f′（x）=2x， 模拟程序的运行，可得
n=1，x=3
执行循环体，x=3﹣ 
=2，n=2
满足条件n＜3，执行循环体，x=2﹣ 
= 
，n=3
不满足条件n＜3，退出循环，输出x的值为 ，即1.75．
故选：B．
【考点精析】关于本题考查的程序框图，需要了解程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明才能得出正确答案．
练习册系列答案
相关题目
【题目】某电子产品公司前四年的年宣传费x（单位：千万元）与年销售量y（单位：百万部）的数据如下表所示：
x（单位：千万元） | 1 | 2 | 3 | 4 |
y（单位：百万部） | 3 | 5 | 6 | 9 |
可以求y关于x的线性回归方程为 
=1.9x+1．
参考公式：回归方程 = 
x+ 
中斜率和截距的最小二乘法估计公式分别为： = 
， = 
﹣ 
．
（1）该公司下一年准备投入10千万元的宣传费，根据所求得的回归方程预测下一年的销售量m：
（2）根据下表所示五个散点数据，求出y关于x的线性回归方程 = x+ ．
x（单位：千万元） | 1 | 2 | 3 | 4 | 10 |
y（单位：百万部） | 3 | 5 | 6 | 9 | m |
并利用小二乘法的原理说明 = x+ 与 =1.9x+1的关系．
