题目内容
15.在平面直角坐标系xOy中,已知圆O:x2+y2=16,点P(1,2),若M,N为圆O上不同的两点,且PM⊥PN,则MN的取值范围是[3$\sqrt{3}$-$\sqrt{5}$,3$\sqrt{3}$+$\sqrt{5}$].分析 如图所示,当四边形PMQN为正方形且MN⊥OP时,|MN|取得最小值或最大值,求出M的坐标即可得出结论.
解答 解:如图所示, 当四边形PMQN为正方形且MN⊥OP时,|MN|取得最小值或最大值.
当四边形PMQN为正方形且MN⊥OP时,|MN|取得最小值或最大值.
设kPM=k,∵∠QPM=45°,∴$\frac{2-k}{1+2k}$=1,解得k=$\frac{1}{3}$.
∴直线PM的方程为:y-2=$\frac{1}{3}$(x-1),化为x-3y+5=0,
代入圆 的方程,化为10y2-30y+9=0,
解得y=$\frac{15+3\sqrt{15}}{10}$或y=$\frac{15-3\sqrt{15}}{10}$.
∴x=3y-5=$\frac{9\sqrt{15}-5}{10}$或$\frac{-9\sqrt{15}-5}{10}$.
∵MN=$\sqrt{2}$PM
∴MNmin=3$\sqrt{3}$-$\sqrt{5}$,MNmax=3$\sqrt{3}$+$\sqrt{5}$.
故答案为:[3$\sqrt{3}$-$\sqrt{5}$,3$\sqrt{3}$+$\sqrt{5}$].
点评 本题考查了向量的平行四边形法则和矩形的定义、满足一定条件取得最小值的转化问题,考查了计算能力,属于难题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
5.复数z=$\frac{3+i}{1-i}$(i为虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.从平行六面体的8个顶点中任取5个顶点为顶点,恰好构成四棱锥的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
10.已知集合A={x||x+1≤2},B={x|y=lg(x2-x-2)},则A∩∁RB( )
| A. | [-1,1] | B. | [-3,-1] | C. | (-1,1] | D. | [-3,-1) |
20.在△ABC中,角A,B,C所对的边分别为a,b,c,已知a=2$\sqrt{3}$,c=2$\sqrt{2}$,1+$\frac{tanA}{tanB}$=$\frac{2c}{b}$.则∠C=( )
| A. | 30° | B. | 135° | C. | 45°或135° | D. | 45° |
4.已知cosα=$\frac{4}{5}$,α∈(-$\frac{π}{2}$,0),则tan($\frac{π}{4}$+$\frac{α}{2}$)的值是( )
| A. | 2 | B. | $\frac{2}{5}$ | C. | -2 | D. | -$\frac{1}{2}$ |
5.一个算法的程序框图如图所示,若运行该程序后输出的结果为$\frac{4}{5}$,则判断框中应填入的条件是( )
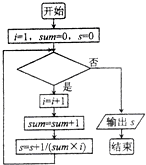

| A. | i≤5? | B. | i≤4? | C. | i≥4? | D. | i≥5? |