题目内容
6.以直角坐标系的原点为极点,x轴正半轴为极轴,建立极坐标系,已知曲线c1的参数方程为$\left\{\begin{array}{l}{x=1+2cosα}\\{y=2+2sinα}\end{array}\right.$(α为参数),直线l的极坐标方程为θ=$\frac{π}{4}$.(1)求曲线c1与直线l的直角坐标方程.
(2)若直线l与曲线c1交于两点A、B,求|AB|.
分析 (1)由cos2α+sin2α=1,可把曲线c1的参数方程$\left\{\begin{array}{l}{x=1+2cosα}\\{y=2+2sinα}\end{array}\right.$(α为参数)化为直角坐标方程;直线l的极坐标方程为θ=$\frac{π}{4}$,可的直线的倾斜角为$\frac{π}{4}$.又经过原点,利用点斜式即可得出.
(2)求出圆心(1,2)到直线y=x的距离d,利用|AB|=2$\sqrt{{r}^{2}-{d}^{2}}$即可得出.
解答 解:(1)曲线c1的参数方程为$\left\{\begin{array}{l}{x=1+2cosα}\\{y=2+2sinα}\end{array}\right.$(α为参数),由cos2α+sin2α=1,可得:曲线C1的直角坐标方程为:(x-1)2+(y-2)2=4;
直线l的极坐标方程为θ=$\frac{π}{4}$,可的直线的倾斜角为$\frac{π}{4}$.又经过原点,∴曲线C2的直角坐标方程为:y=x.
(2)∵圆心(1,2)到直线y=x的距离d=$\frac{\sqrt{2}}{2}$,
∴|AB|=2$\sqrt{4-\frac{1}{2}}$=$\sqrt{14}$.
点评 本题考查了参数方程化为直角坐标方程、极坐标方程化为直角坐标方程、直线与圆相交弦长问题、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.下列说法正确的是( )
| A. | 命题“若x=y,则sinx=siny”的否命题为真命题 | |
| B. | “直线x-ay=0与直线x+ay=0互相垂直”的充分条件是“a=1” | |
| C. | 命题“?x∈R,x2+x+1<0”的否定是“?x∈R,x2+x+1>0” | |
| D. | 命题:若x2=1,则x=1或x=-1的逆否命题为:若x≠1或x≠-1,则x2≠1 |
1.已知 m、n 是两条不重合的直线,α、β、γ是三个互不重合的平面,则下列命题中 正确的是( )
| A. | 若 m∥α,n∥α,则 m∥n | B. | 若α⊥γ,β⊥γ,则 α∥β | ||
| C. | 若m⊥α,n⊥α,则 m∥n | D. | 若 m∥α,m∥β,则 α∥β |
18.已知集合A={-2,a},B={2a,b},若A∩B={1},则A∪B=( )
| A. | {-2,1,3} | B. | {-2,1,2} | C. | {-2,1} | D. | {-2,1,5} |
16.各项均为正数的等差数列{an}中,a4a9=36,则前12项和S12的最小值为( )
| A. | 78 | B. | 48 | C. | 60 | D. | 72 |
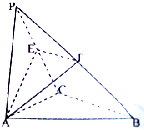 如图,在三棱锥P-ABC中,AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E、F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
如图,在三棱锥P-ABC中,AC⊥BC,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E、F分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.