Question

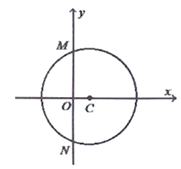
【题目】已知圆心在x轴正半轴上的圆C与直线相切，与y轴交于M，N两点，且．

Ⅰ求圆C的标准方程；

Ⅱ过点的直线l与圆C交于不同的两点D，E，若时，求直线l的方程；

Ⅲ已知Q是圆C上任意一点，问：在x轴上是否存在两定点A，B，使得？若存在，求出A，B两点的坐标；若不存在，请说明理由．

Answer 1

【答案】（I）；（II）或；（III）存在，或，满足题意.

【解析】

设圆C的方程为，利用点C到直线的距离为，求出a，即可求圆C的标准方程；

Ⅱ设直线l的方程为即，则由题意可知，圆心C到直线l的距离，即可求出k的值，

Ⅲ方法一：假设在x轴上存在两定点，，设是圆C上任意一点，由题意可得则，即可求出a，b的值，

方法二：设是圆C上任意一点，由得，对照圆C的标准方程即，可得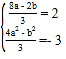，解得即可．

解：Ⅰ由题意知圆心，且，

由知中，，，则，

于是可设圆C的方程为

又点C到直线的距离为，

所以或舍，

故圆C的方程为，

Ⅱ设直线l的方程为即，则由题意可知，圆心C到直线l的距离，

故，解得，

又当时满足题意，

因此所求的直线方程为或，

Ⅲ方法一：假设在x轴上存在两定点，，设是圆C上任意一点，则即，

则，

令，

解得或，

因此存在，，或，满足题意，

方法二：设是圆C上任意一点，

由得，

化简可得，

对照圆C的标准方程即，

可得，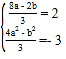

解得解得或，

因此存在，或，满足题意．