题目内容
【题目】已知向量
，
，
，函数
.
（1）求函数
的对称中心;
（2）设锐角
三个内角
所对的边分别为
，若
求
和c
【答案】（1）
；（2）
,
.
【解析】
（1）利用平面向量数量积的运算，三角函数恒等变换的应用化简函数解析式可得f（x）
，利用三角函数的对称中心即可得解．（2）由（1）知可得
，结合A的范围可求
，解法一：由余弦定理解得c的值，解法二：由正弦定理解得sinB，由B是锐角，可求cosB，利用三角形内角和定理，两角和的正弦函数公式可求sinC，根据正弦定理即可解得c的值．
，
令
,解x=
故对称中心为
.
（2）.
∵
，∴
，
∴
，∴.
方法一 由余弦定理得
，
解得
或
.
若，则
，
∴
为钝角，这与
为锐角三角形不符，故
.
∴.
方法二 由正弦定理得
，解得
.
∵是锐角，∴
，
∵
，
∴
，
由正弦定理得
，解得.
名校课堂系列答案
【题目】已知双曲线 
与双曲线 
的离心率相同，且双曲线C2的左、右焦点分别为F1 ， F2 ， M是双曲线C2一条渐近线上的某一点，且OM⊥MF2 ， 
，则双曲线C2的实轴长为（ ）
A.4
B.
C.8
D.
【题目】某种产品的质量以其质量指标值衡量，并依据质量指标值划分等极如下表：
质量指标值m | m＜185 | 185≤m＜205 | m≥205 |
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件，检测后得到如下的频率分布直方图：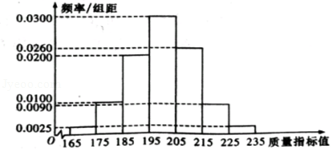
（Ⅰ）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定？
（Ⅱ）在样本中，按产品等极用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；
（III）该企业为提高产品质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值X近似满足X～N（218，140}），则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？
