题目内容
7.已知集合A={-1,0,2},B={x|x=2n-1,n∈Z},则A∩B={-1}.分析 观察发现集合B为所有的奇数集,所以找出集合A解集中的奇数解即为两集合的交集.
解答 解:由集合A={-1,0,2},
根据集合A中的关系式x=2n-1,n∈Z,得到集合B为所有的奇数集,
则集合A∩B={-1}.
故答案为:{-1}.
点评 此题属于以不等式解集中的奇数解为平台,考查了交集的运算,是一道基础题.也是高考中常考的题型.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
17.某班的一次数学考试后,按学号统计前20名同学的考试成绩如茎叶图所示,则该样本数据的中位数为( )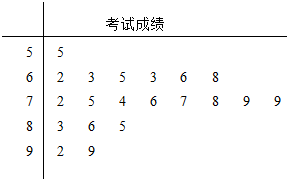

| A. | 74.5 | B. | 75 | C. | 75.5 | D. | 76 |
2. 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )
 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为( )| A. | 100 | B. | 120 | C. | 130 | D. | 390 |