题目内容
20.在[0,1]上任取一数a,在[1,2]上任取一数b,则点(a,b)满足a2+b2≤2的概率为$\frac{π-2}{4}$.分析 根据几何概型,只要求出在两个区间内随机取两个数分别记为a,b,对应平面区域的面积,再求出满足条件a2+b2≤2对应的平面区域的面积,然后代入几何概型公式,即可求解.
解答 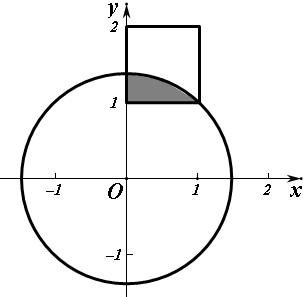 解:[0,1]上任取一数a,在[1,2]上任取一数b,则(a,b)点对应的区域如图中正方形所示
解:[0,1]上任取一数a,在[1,2]上任取一数b,则(a,b)点对应的区域如图中正方形所示
若a2+b2≤2,
则(a,b)点对应的区域在以原点为圆心,以$\sqrt{2}$为半径的圆上或圆内
如图中阴影部分所示,∵S正方形=1×1=1,S阴影=$\frac{π(\sqrt{2})^{2}}{8}-\frac{1}{2}$=$\frac{π}{4}-\frac{1}{2}$,
故在[0,1]上任取一数a,在[1,2]上任取一数b,使得a2+b2≤2的概率P=$\frac{{S}_{阴影}}{{S}_{正方形}}$=$\frac{\frac{π}{4}-\frac{1}{2}}{1}=\frac{π-2}{4}$;
故答案为:$\frac{π-2}{4}$.
点评 本题考查几何概型;其概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
相关题目
12.设函数f(x)=3sin(ωx+$\frac{π}{6}$)(ω>0)的周期是π,则( )
| A. | f(x)的图象过点(0,$\frac{1}{2}$) | |
| B. | f(x)在[$\frac{π}{12}$,$\frac{2π}{3}$]上是减函数 | |
| C. | f(x)的一个对称中心是($\frac{5π}{12}$,0) | |
| D. | 将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数y=3sinωx的图象 |
9.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,且$\overrightarrow{b}$•(2$\overrightarrow{a}$+$\overrightarrow{b}$)=1,则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值是( )
| A. | -$\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | -$\frac{\sqrt{2}}{4}$ | D. | $\frac{1}{3}$ |