题目内容
2.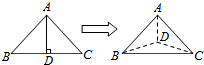 如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折
如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC
其中正确的是( )
| A. | ①②④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
分析 设等腰直角三角形△ABC的腰为a,则斜边BC=$\sqrt{2}$a,
①利用面面垂直的性质定理易证BD⊥平面ADC,又AC?平面ADC,从而可知BD⊥AC,可判断①;
②依题意及设法可知,AB=AC=a,BD=CD=$\frac{\sqrt{2}}{2}$a,利用勾股定理可求得BC=$\sqrt{2}$•$\frac{\sqrt{2}}{2}$a=a,从而可判断②;
③又因为DA=DB=DC,根据正三棱锥的定义判断;
④作出平面ADC与平面ABC的二面角的平面角,利用BD⊥平面ADC可知,∠BDF为直角,∠BFD不是直角,从而可判断④.
解答 解:解:设等腰直角三角形△ABC的腰为a,则斜边BC=$\sqrt{2}$a,
①∵D为BC的中点,∴AD⊥BC,
又平面ABD⊥平面ACD,平面ABD∩平面ACD=AD,BD⊥AD,BD?平面ABD,
∴BD⊥平面ADC,又AC?平面ADC,
∴BD⊥AC,故①正确;
②由A知,BD⊥平面ADC,CD?平面ADC,
∴BD⊥CD,又BD=CD=$\frac{\sqrt{2}}{2}$a,
∴由勾股定理得:BC=$\sqrt{2}$•$\frac{\sqrt{2}}{2}$a=a,又AB=AC=a,
∴△ABC是等边三角形,故②正确;
③∵△ABC是等边三角形,DA=DB=DC,
∴三棱锥D-ABC是正三棱锥,故③正确.
④∵△ADC为等腰直角三角形,取斜边AC的中点F,则DF⊥AC,又△ABC为等边三角形,连接BF,则BF⊥AC,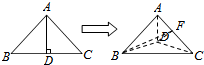
∴∠BFD为平面ADC与平面ABC的二面角的平面角,
由BD⊥平面ADC可知,∠BDF为直角,∠BFD不是直角,故平面ADC与平面ABC不垂直,故④错误;
综上所述,正确的结论是①②③.
故选:B.
点评 本题考查命题的真假判断与应用,着重考查线面垂直的判定与应用,考查二面角的作图与运算,属于中档题.

 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案| A. | f(x)的图象过点(0,$\frac{1}{2}$) | |
| B. | f(x)在[$\frac{π}{12}$,$\frac{2π}{3}$]上是减函数 | |
| C. | f(x)的一个对称中心是($\frac{5π}{12}$,0) | |
| D. | 将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数y=3sinωx的图象 |