题目内容
7.已知函数f(x)=2sinx+2sin(x-$\frac{π}{3}$)(1)求f(x)的单调递增区间;
(2)在△ABC中,内角A,B,C所对的边分别为a,b,c,已知f(A)=$\sqrt{3}$,a=$\sqrt{3}$b,证明:C=3B.
分析 (1)根据两角差的正弦公式即可将f(x)变成f(x)=$2\sqrt{3}sin(x-\frac{π}{6})$,根据正弦函数的单调增区间即可求出函数f(x)的单调增区间;
(2)A带入f(x)便可得出sin(A$-\frac{π}{6}$)=$\frac{1}{2}$,从而可得到A=$\frac{π}{3}$,而由正弦定理及a=$\sqrt{3}b$即可得到sinA=$\sqrt{3}$sinB,从而得到sinB=$\frac{1}{2}$,B=$\frac{π}{6}$,从而得到C=$\frac{π}{2}$,从而得出C=3B.
解答 解:(1)f(x)=2sinx+2sin(x-$\frac{π}{3}$)=2sinx+2(sinxcos$\frac{π}{3}$-cosxsin$\frac{π}{3}$)=2sinx+sinx-$\sqrt{3}$cosx=3sinx-$\sqrt{3}$cosx=2$\sqrt{3}$($\frac{\sqrt{3}}{2}$sinx-$\frac{1}{2}$cosx)=2$\sqrt{3}$sin(x-$\frac{π}{6}$);
令-$\frac{π}{2}$+2kπ≤x-$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,k∈Z,得到-$\frac{π}{3}$+2kπ≤x≤$\frac{2π}{3}$+2kπ,k∈Z;
则f(x)的单调递增区间为[-$\frac{π}{3}$+2kπ,$\frac{2π}{3}$+2kπ],k∈Z;
(2)证明:由f(A)=2$\sqrt{3}$sin(A-$\frac{π}{6}$)=$\sqrt{3}$,得到sin(A-$\frac{π}{6}$)=$\frac{1}{2}$;
∵0<A<π;
∴$-\frac{π}{6}<A-\frac{π}{6}<\frac{5π}{6}$;
∴$A-\frac{π}{6}=\frac{π}{6}$;
∴$A=\frac{π}{3}$;
根据正弦定理,由a=$\sqrt{3}b$得sinA=$\sqrt{3}sinB$;
∴$sinB=\frac{1}{2}$;
$0<B<\frac{2π}{3}$;
∴$B=\frac{π}{6}$;
∴$C=π-A-B=π-\frac{π}{3}-\frac{π}{6}=\frac{π}{2}$;
∴C=3B.
点评 考查两角差的正弦公式,三角形的内角和为π,正弦函数的单调区间,复合函数单调区间的求法,以及正弦定理,已知三角函数值求角.

 阅读快车系列答案
阅读快车系列答案| A. | (-2,-4) | B. | (2,4) | C. | (6,10) | D. | (-6,-10) |
| A. | f(x)的图象过点(0,$\frac{1}{2}$) | |
| B. | f(x)在[$\frac{π}{12}$,$\frac{2π}{3}$]上是减函数 | |
| C. | f(x)的一个对称中心是($\frac{5π}{12}$,0) | |
| D. | 将f(x)的图象向右平移$\frac{π}{6}$个单位得到函数y=3sinωx的图象 |
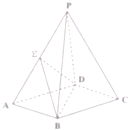 如图,在四棱锥P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC,求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC,求证: