题目内容
12.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别是F1,F2,过F2作直线PF2⊥F1F2,交双曲线C于P,若△PF1F2为等腰直角三角形,则双曲线C的离心率为( )| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{2}$+2 |
分析 通过双曲线的定义及勾股定理,利用离心率的公式直接计算即可.
解答 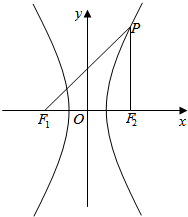 解:如图,F1F2=PF2,
解:如图,F1F2=PF2,
由双曲线的定义可知:
PF1=PF2+2a=2a+2c,
又∵△PF1F2为等腰直角三角形,
∴PF1=$\sqrt{2}$PF2=2$\sqrt{2}$c,
即2a=2$\sqrt{2}$c-2c,
∴e=$\frac{c}{a}$=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1,
故选:C.
点评 本题考查求双曲线的离心率,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
3.函数f(x)=$\frac{\sqrt{2x+1}}{x-3}$的定义域为( )
| A. | {x|x≥-$\frac{1}{2}$} | B. | {x|x>-$\frac{1}{2}$且x≠3} | C. | {x|x≥-$\frac{1}{2}$且x≠3} | D. | {x|x≠3} |
4.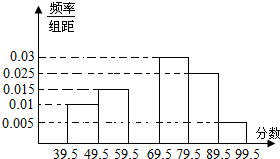 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布表和频率分布直方图如下,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布表和频率分布直方图如下,回答下列问题:
(1)分别求出a,b,x,y的值,并补全频率分布直方图;
(2)估计这次环保知识竞赛平均分;
(3)若从所有参加环保知识竞赛的学生中随机抽取一人采访,抽到的学生成绩及格的概率有多大?
 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布表和频率分布直方图如下,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布表和频率分布直方图如下,回答下列问题:| 分组 | 人数 | 频率 |
| [39.5,49.5) | a | 0.10 |
| [49.5,59.5) | 9 | x |
| [59.5,69.5) | b | 0.15 |
| [69.5,79.5) | 18 | 0.30 |
| [79.5,89.5) | 15 | y |
| [89.5,99.5] | 3 | 0.05 |
(2)估计这次环保知识竞赛平均分;
(3)若从所有参加环保知识竞赛的学生中随机抽取一人采访,抽到的学生成绩及格的概率有多大?
1.已知线段PQ的中点为M(0,4),若点P在直线x+y-2=0上运动,则点Q的轨迹方程是( )
| A. | x+y-6=0 | B. | x+y+6=0 | C. | x-y-2=0 | D. | x-y+2=0 |
2.为了得到函数$y={(\frac{1}{3})^x}$的图象,可以把函数$y=3×{(\frac{1}{3})^x}$的图象( )
| A. | 向左平移1个单位 | B. | 向右平移1个单位 | C. | 向左平移3个单位 | D. | 向右平移3个单位 |