题目内容
5.在△ABC中,角A,B,C的对边分别是a,b,c,若(2a+c)cosB+bcosC=0.(1)求角B的大小;
(2)若a=3,△ABC的面积为$\frac{{3\sqrt{3}}}{2}$,求$\overrightarrow{AB}•\overrightarrow{BC}$的值.
分析 (1)由(2a+c)cosB+bcosC=0.利用正弦定理可得:2sinAcosB+sinCcosB+sinBcosC=0,化简即可解出.(2)由a=3,△ABC的面积为$\frac{{3\sqrt{3}}}{2}$,可得$\frac{3\sqrt{3}}{2}$=$\frac{1}{2}acsinB$=$\frac{1}{2}×3c•sin\frac{2π}{3}$,解得c.可得$\overrightarrow{AB}•\overrightarrow{BC}$=-cacosB.
解答 解:(1)由(2a+c)cosB+bcosC=0.
利用正弦定理可得:2sinAcosB+sinCcosB+sinBcosC=0,
化为2sinAcosB=-sin(C+B)=-sinA,
∵sinA≠0,
∴cosB=-$\frac{1}{2}$,B∈(0,π).
解得B=$\frac{2π}{3}$.
(2)∵a=3,△ABC的面积为$\frac{{3\sqrt{3}}}{2}$,
∴$\frac{3\sqrt{3}}{2}$=$\frac{1}{2}acsinB$=$\frac{1}{2}×3c•sin\frac{2π}{3}$,解得c=2.
∴$\overrightarrow{AB}•\overrightarrow{BC}$=-cacosB=-2×3×$cos\frac{2π}{3}$=3.
点评 本题考查了正弦定理的应用、两角和差公式、三角形面积计算公式、向量数量积运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
20.下列函数中,既是奇函数又在区间(0,+∞)上单调递增的函数是( )
| A. | y=x+x-1 | B. | y=x3+x | C. | y=2x+log2x | D. | $y={x^{\frac{1}{2}}}$ |
16.已知椭圆C的中心在原点,左焦点F1,右焦点F2均在x轴上,A为椭圆的右顶点,B为椭圆短轴的端点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,则此椭圆的离心率等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
20.已知数列{an},点{n,an}在函数$f(x)=sin(πx+\frac{π}{3})$的图象上,则a2015的值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
15.命题“关于x的不等式x2-ax+4>0在(0,+∞)上恒成立”的否定是( )
| A. | ?x∈(-∞,0),x2-ax+4>0 | B. | ?x∈(-∞,0),x2-ax+4>0 | ||
| C. | ?x∈(0,+∞),x2-ax+4≤0 | D. | ?x∈(0,+∞),x2-ax+4≤0 |
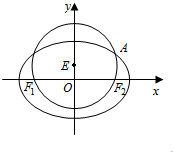 已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且$\overrightarrow{MN}$=λ$\overrightarrow{OA}$(λ≠0)
已知圆E:x2+(y-$\frac{1}{2}$)2=$\frac{9}{4}$经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点F1,F2,且与椭圆C在第一象限的交点为A,且F1,E,A三点共线,直线l交椭圆C于M,N两点,且$\overrightarrow{MN}$=λ$\overrightarrow{OA}$(λ≠0)