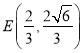题目内容
【题目】在四棱锥PABCD中,AD∥BC,平面PAC⊥平面ABCD,AB=AD=DC=1,
∠ABC=∠DCB=60,E是PC上一点.
(Ⅰ)证明:平面EAB⊥平面PAC;
(Ⅱ)若△PAC是正三角形,且E是PC中点,求三棱锥AEBC的体积.

【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(Ⅰ)在等腰梯形ABCD中,由条件得AB⊥AC,又平面PAC⊥平面ABCD,故得AB⊥平面PAC,从而可得平面EAB⊥平面PAC.(Ⅱ)根据![]() 求解,由(Ⅰ)得AB⊥平面PAC,故AB为三棱锥BEAC的高,在正△PAC中可得S△EAC=
求解,由(Ⅰ)得AB⊥平面PAC,故AB为三棱锥BEAC的高,在正△PAC中可得S△EAC=![]() S△PAC,根据体积公式可求得三棱锥的体积.
S△PAC,根据体积公式可求得三棱锥的体积.
试题解析:
(Ⅰ)证明:依题意得四边形ABCD是底角为60的等腰梯形,
∴∠BAD=∠ADC=120.
∵ AD=DC,
∴∠DAC=∠DCA=30,
∴∠BAC=∠BAD∠DAC=12030=90,
∴AB⊥AC.
∵平面PAC⊥平面ABCD, 平面PAC∩平面ABCD=AC,
∴AB⊥平面PAC.
又AB平面EAB,
∴平面EAB⊥平面PAC.
(Ⅱ)由(Ⅰ)及已知得,在Rt△ABC中,∠ABC=60,AB=1,
∴AC= ABtan60=![]() ,且BC=2AB=2.
,且BC=2AB=2.
又AB⊥平面PAC,
∴AB是三棱锥BEAC的高.
∵E是PC的中点,
∴S△EAC=![]() S△PAC=
S△PAC=![]() .
.
∴三棱锥AEBC的体积为![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目