题目内容
4.已知函数f(x)=x3+ax2+b(a,b∈R).(1)试讨论f(x)的单调性;
(2)若b=c-a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(-∞,-3)∪(1,$\frac{3}{2}$)∪($\frac{3}{2}$,+∞),求c的值.
分析 (1)求导数,分类讨论,利用导数的正负,即可得出f(x)的单调性;
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(-$\frac{2a}{3}$)=$\frac{4}{27}{a}^{3}$+b,则函数f(x)有三个不同的零点等价于f(0)f(-$\frac{2a}{3}$)=b($\frac{4}{27}{a}^{3}$+b)<0,进一步转化为a>0时,$\frac{4}{27}{a}^{3}$-a+c>0或a<0时,$\frac{4}{27}{a}^{3}$-a+c<0.设g(a)=$\frac{4}{27}{a}^{3}$-a+c,利用条件即可求c的值.
解答 解:(1)∵f(x)=x3+ax2+b,
∴f′(x)=3x2+2ax,
令f′(x)=0,可得x=0或-$\frac{2a}{3}$.
a=0时,f′(x)>0,∴f(x)在(-∞,+∞)上单调递增;
a>0时,x∈(-∞,-$\frac{2a}{3}$)∪(0,+∞)时,f′(x)>0,x∈(-$\frac{2a}{3}$,0)时,f′(x)<0,
∴函数f(x)在(-∞,-$\frac{2a}{3}$),(0,+∞)上单调递增,在(-$\frac{2a}{3}$,0)上单调递减;
a<0时,x∈(-∞,0)∪(-$\frac{2a}{3}$,+∞)时,f′(x)>0,x∈(0,-$\frac{2a}{3}$)时,f′(x)<0,
∴函数f(x)在(-∞,0),(-$\frac{2a}{3}$,+∞)上单调递增,在(0,-$\frac{2a}{3}$)上单调递减;
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(-$\frac{2a}{3}$)=$\frac{4}{27}{a}^{3}$+b,
则函数f(x)有三个不同的零点等价于f(0)>0,且f(-$\frac{2a}{3}$)<0,
∴b>0且$\frac{4}{27}{a}^{3}$+b<0,
∵b=c-a,
∴a>0时,$\frac{4}{27}{a}^{3}$-a+c>0或a<0时,$\frac{4}{27}{a}^{3}$-a+c<0.
设g(a)=$\frac{4}{27}{a}^{3}$-a+c,
∵函数f(x)有三个不同的零点时,a的取值范围恰好是(-∞,-3)∪(1,$\frac{3}{2}$)∪($\frac{3}{2}$,+∞),
∴在(-∞,-3)上,g(a)<0且在(1,$\frac{3}{2}$)∪($\frac{3}{2}$,+∞)上g(a)>0均恒成立,
∴g(-3)=c-1≤0,且g($\frac{3}{2}$)=c-1≥0,
∴c=1,
此时f(x)=x3+ax2+1-a=(x+1)[x2+(a-1)x+1-a],
∵函数有三个零点,
∴x2+(a-1)x+1-a=0有两个异于-1的不等实根,
∴△=(a-1)2-4(1-a)>0,且(-1)2-(a-1)+1-a≠0,
解得a∈(-∞,-3)∪(1,$\frac{3}{2}$)∪($\frac{3}{2}$,+∞),
综上c=1.
点评 本题考查导数知识的综合运用,考查函数的单调性,考查函数的零点,考查分类讨论的数学思想,难度大.

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案| A. | $\frac{3}{4}$+$\frac{1}{2π}$ | B. | $\frac{1}{2}$+$\frac{1}{π}$ | C. | $\frac{1}{4}$-$\frac{1}{2π}$ | D. | $\frac{1}{2}$-$\frac{1}{π}$ |
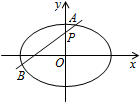 如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的离心率是$\frac{\sqrt{2}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2$\sqrt{2}$.
如图,椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的离心率是$\frac{\sqrt{2}}{2}$,过点P(0,1)的动直线l与椭圆相交于A、B两点,当直线l平行于x轴时,直线l被椭圆E截得的线段长为2$\sqrt{2}$.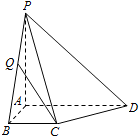 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=$\frac{π}{2}$,PA=AD=2,AB=BC=1.
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=$\frac{π}{2}$,PA=AD=2,AB=BC=1.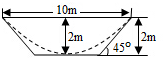 如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为1.2.
如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线所示),则原始的最大流量与当前最大流量的比值为1.2.