题目内容

18．已知等差数列{an}的公差d≠0，且a1，a3，a9构成等比数列{bn}的前3项，则$\frac{a_9}{a_3}$=3；又若d=2，则数列{bn}的前n项的和Sn=3n-1．

分析 由等比数列的性质和等差数列的通项公式可得d=a1，再由等比数列的定义和等差数列的通项公式，以及等比数列的求和公式计算可得．

解答 解：由题意可得a32=a1a9，
即为（a1+2d）2=a1（a1+8d），
即4d2=4a1d，（d≠0），
可得d=a1，$\frac{{a}_{9}}{{a}_{3}}$=$\frac{d+8d}{d+2d}$=3；
若d=2，则a1=2，a3=2+4=6，
即有等比数列{bn}的公比为q=3，
和Sn=$\frac{2（1-{3}^{n}）}{1-3}$=3n-1．
故答案为：3，3n-1．

点评 本题考查等差数列和等比数列的通项公式的运用，等比数列的求和公式的运用，考查运算能力，属于中档题．

练习册系列答案
相关题目
8．下列函数在（-∞，0）∪（0，+∞）上既是偶函数，又在（0，+∞）上单调递增的是（　　）
A．y=-x2B．y=x-1C．y=log2|x|D．y=-2x
9．以下四个命题中是真命题的有①②（填序号）．
①命题“若xy=1，则x，y互为倒数”的逆命题；
②命题“面积相等的两个三角形全等”的否命题；
③命题“若m≤1，则0.005×20×2+0.0025×20=0.25有实根”的逆否命题；
④命题“若A∩B=B，则A⊆B”的逆否命题．
6．下列四种说法：
①函数y=$\frac{{x}^{2}-x+4}{x-1}（x＞1）$的最小值为5；
②等差数列{an}中，a1，a3，a4成等比数列，则公比为$\frac{1}{2}$；
③已知a＞0，b＞0，a+b=1，则$\frac{2}{a}+\frac{3}{b}$的最小值为5+2$\sqrt{6}$；
④在平面直角坐标系xOy中，已知平面区域A={（x，y）|x+y≤1，x≥0，y≥0}，则平面区域B={（x+y，x-y）|（x，y）∈A}的面积是1．
其中正确的命题为①③④（填上所有正确命题的序号）
13．计算：
（1）（2$\frac{7}{9}$）0.5+0.5-2+（2$\frac{10}{27}$）${\;}^{-\frac{1}{3}}$-3π0+$\frac{37}{48}$
（2）lg$\frac{1}{2}$-lg$\frac{5}{8}$+lg12.5-log29•log278．
3．求满足$\frac{1}{2}$＜sinθ≤$\frac{\sqrt{3}}{2}$的θ的取值范围．
10．设函数g（x）=x2f（x），若函数f（x）为定义在R上的奇函数，其导函数为f′（x），对任意实数x满足x2f′（x）＞2xf（-x），则不等式g（x）＜g（1-3x）的解集是（　　）
A．$（{\frac{1}{4}，+∞}）$B．（0，$\frac{1}{4}$）C．$（{-∞，\frac{1}{4}}）$D．$（{-∞，\frac{1}{4}}）∪（{\frac{1}{4}，+∞}）$
7．如图，给出了偶函数y=f（x）的局部图象，根据图象信息下列结论正确的是（　　）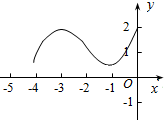  
A．f（-1）-f（2）＞0B．f（1）-f（-2）=0C．f（1）-f（2）＜0D．f（-1）+f（2）＜0
8．已知四边形ABCD为平行四边形，点A的坐标为（-1，2），点C在第二象限，$\overrightarrow{AB}=（{2，2}），且\overrightarrow{AB}与\overrightarrow{AC}$的夹角为$\frac{π}{4}，\overrightarrow{AB}•\overrightarrow{AC}$=2．
（I）求点D的坐标；
（II）当m为何值时，$\overrightarrow{AC}+m\overrightarrow{AB}与\overrightarrow{BC}$垂直．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网