题目内容
8．下列函数在（-∞，0）∪（0，+∞）上既是偶函数，又在（0，+∞）上单调递增的是（ ）| A． | y=-x2 | B． | y=x-1 | C． | y=log2|x| | D． | y=-2x |
分析 根据 y=-x2 、y=-2x、y=x-1在（0，+∞）上单调递减，故排除A、B、D；再根据y=log2|x|是偶函数，且在在（0，+∞）上单调递增，从而得出结论．
解答 解：由于y=-x2 、y=-2x、y=x-1在（0，+∞）上单调递减，故排除A、B、D；
再根据y=log2|x|是偶函数，且在在（0，+∞）上单调递增，故满足条件，
故选：C．
点评 本题主要考查函数的奇偶性、单调性的判断，属于基础题．
练习册系列答案
相关题目
6．在直棱柱（侧棱垂直于底面）ABC-A1B1C1中，点D为BC的中点，BC=4，AB=AC=$\sqrt{7}$，AA1=3，则三棱锥C1-AB1D的高为（ ）
| A． | $\sqrt{3}$ | B． | $\frac{6\sqrt{13}}{13}$ | C． | $\frac{12\sqrt{13}}{13}$ | D． | $\frac{\sqrt{39}}{13}$ |
19．若a，b，c＞0，且$a（a+b+c）+bc=4+2\sqrt{3}$，则2a+b+c的最小值为（ ）
| A． | $\sqrt{3}-1$ | B． | $2\sqrt{3}+2$ | C． | $\sqrt{3}+1$ | D． | $2\sqrt{3}-2$ |
3．某连锁经营公司的5个零售店某月的销售额和利润额资料如表：
（1）若销售额和利润额具有线性相关关系，用最小乘法计算利润额y对销售额x的回归直线方程；
（2）若商店F此月的销售额为1亿1千万元，试用（1）中求得的回归方程，估测其利润．（精确到百万元）
| 商店名称 | A | B | C | D | E |
| 销售额（x）/千万元 | 3 | 5 | 6 | 7 | 9 |
| 利润（y）/百万元 | 2 | 3 | 3 | 4 | 5 |
（2）若商店F此月的销售额为1亿1千万元，试用（1）中求得的回归方程，估测其利润．（精确到百万元）
20．
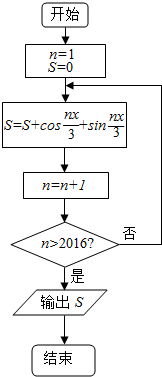如图所示程序框图中，输出S=（ ）
如图所示程序框图中，输出S=（ ）| A． | -1 | B． | 0 | C． | 1 | D． | $\sqrt{3}$ |