题目内容
8.已知四边形ABCD为平行四边形,点A的坐标为(-1,2),点C在第二象限,$\overrightarrow{AB}=({2,2}),且\overrightarrow{AB}与\overrightarrow{AC}$的夹角为$\frac{π}{4},\overrightarrow{AB}•\overrightarrow{AC}$=2.(I)求点D的坐标;
(II)当m为何值时,$\overrightarrow{AC}+m\overrightarrow{AB}与\overrightarrow{BC}$垂直.
分析 (I)设C(x,y),D(m,n).$\overrightarrow{AC}$=(x+1,y-2),利用向量夹角公式可得(x+1)2+(y-2)2=1.①又$\overrightarrow{AB}•\overrightarrow{AC}$=2(x+1)+2(y-2)=2,联立解出C坐标.又$\overrightarrow{CD}=\overrightarrow{BA}$,可得(m+1,n-3)=(-2,2),解得m,n.
(II)由(I)可知:$\overrightarrow{AC}$=(0,1),由于$\overrightarrow{AC}+m\overrightarrow{AB}与\overrightarrow{BC}$垂直.可得($\overrightarrow{AC}+m\overrightarrow{AB})$$•\overrightarrow{BC}$=0,解出即可.
解答 解:(I)设C(x,y),D(m,n).$\overrightarrow{AC}$=(x+1,y-2),
∵$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角为$\frac{π}{4},\overrightarrow{AB}•\overrightarrow{AC}$=2.
∴$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}$=$\frac{2}{\sqrt{{2}^{2}+{2}^{2}}\sqrt{(x+1)^{2}+(y-2)^{2}}}$=$\frac{\sqrt{2}}{2}$,化为(x+1)2+(y-2)2=1.①
又$\overrightarrow{AB}•\overrightarrow{AC}$=2(x+1)+2(y-2)=2,化为x+y=2.②
联立①②解得$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$.
又点C在第二象限,∴C(-1,3).
又$\overrightarrow{CD}=\overrightarrow{BA}$,
∴(m+1,n-3)=(-2,2),解得m=-3,n=1.
∴D(-3,1).
(II)由(I)可知:$\overrightarrow{AC}$=(0,1),
∴$\overrightarrow{AC}+m\overrightarrow{AB}$=(2m,2m+1),$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$=(-2,-1).
∵$\overrightarrow{AC}+m\overrightarrow{AB}与\overrightarrow{BC}$垂直.
∴($\overrightarrow{AC}+m\overrightarrow{AB})$$•\overrightarrow{BC}$=-4m-(2m+1)=0,解得m=$-\frac{1}{6}$.
点评 本题考查了向量夹角公式、数量积运算性质、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.

 金钥匙试卷系列答案
金钥匙试卷系列答案①若a>|b|,则a2>b2
②若a>b,c>d,则a-c>b-d
③若a>b,c>d,则ac>bd
④若a>b>o,则$\frac{c}{a}$>$\frac{c}{b}$.
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
| A. | y=log2(x+5) | B. | $y={({\frac{1}{3}})^x}$ | C. | y=-$\sqrt{x+2}$ | D. | y=$\frac{1}{x}$-x |
| A. | {3} | B. | {2,3} | C. | ∅ | D. | {0,1,2,3} |
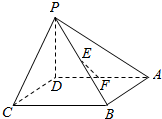 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=2a,E是PB的中点,F是AD的中点,求证:EF⊥平面PCB.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=2a,E是PB的中点,F是AD的中点,求证:EF⊥平面PCB.