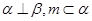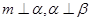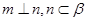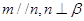题目内容
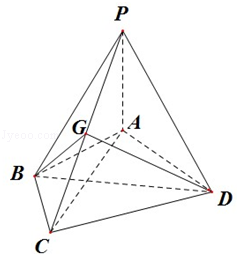
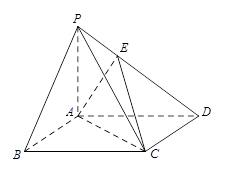
(2013•浙江)如图,在四棱锥P﹣ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=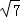 ,PA=
,PA=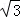 ,∠ABC=120°,G为线段PC上的点.
,∠ABC=120°,G为线段PC上的点.
(Ⅰ)证明:BD⊥平面PAC;
(Ⅱ)若G是PC的中点,求DG与PAC所成的角的正切值;
(Ⅲ)若G满足PC⊥面BGD,求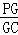 的值.
的值.
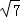 ,PA=
,PA=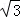 ,∠ABC=120°,G为线段PC上的点.
,∠ABC=120°,G为线段PC上的点.(Ⅰ)证明:BD⊥平面PAC;
(Ⅱ)若G是PC的中点,求DG与PAC所成的角的正切值;
(Ⅲ)若G满足PC⊥面BGD,求
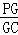 的值.
的值.
(1)见解析 (2) (3)
(3)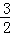
 (3)
(3)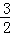
(Ⅰ)证明:∵在四棱锥P﹣ABCD中,PA⊥面ABCD,∴PA⊥BD.
∵AB=BC=2,AD=CD=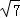 ,设AC与BD的交点为O,则BD是AC的中垂线,故O为AC的中点,且BD⊥AC.
,设AC与BD的交点为O,则BD是AC的中垂线,故O为AC的中点,且BD⊥AC.
而PA∩AC=A,∴BD⊥面PAC.
(Ⅱ)若G是PC的中点,O为AC的中点,则GO平行且等于 PA,故由PA⊥面ABCD,可得GO⊥面ABCD,
PA,故由PA⊥面ABCD,可得GO⊥面ABCD,
∴GO⊥OD,故OD⊥平面PAC,故∠DGO为DG与平面PAC所成的角.
由题意可得,GO= PA=
PA= .
.
△ABC中,由余弦定理可得AC2=AB2+BC2﹣2AB•BC•cos∠ABC=4+4﹣2×2×2×cos120°=12,
∴AC=2 ,OC=
,OC= .
.
∵直角三角形COD中,OD= =2,
=2,
∴直角三角形GOD中,tan∠DGO= =
= .
.
(Ⅲ)若G满足PC⊥面BGD,∵OG?平面BGD,∴PC⊥OG,且 PC=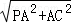 =
= .
.
由△COG∽△PCA,可得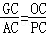 ,即
,即  ,解得GC=
,解得GC= ,
,
∴PG=PC﹣GC=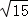 ﹣
﹣ =
=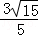 ,∴
,∴ =
=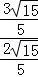 =
=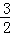 .
.
∵AB=BC=2,AD=CD=
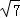 ,设AC与BD的交点为O,则BD是AC的中垂线,故O为AC的中点,且BD⊥AC.
,设AC与BD的交点为O,则BD是AC的中垂线,故O为AC的中点,且BD⊥AC.而PA∩AC=A,∴BD⊥面PAC.
(Ⅱ)若G是PC的中点,O为AC的中点,则GO平行且等于
 PA,故由PA⊥面ABCD,可得GO⊥面ABCD,
PA,故由PA⊥面ABCD,可得GO⊥面ABCD,∴GO⊥OD,故OD⊥平面PAC,故∠DGO为DG与平面PAC所成的角.
由题意可得,GO=
 PA=
PA= .
.△ABC中,由余弦定理可得AC2=AB2+BC2﹣2AB•BC•cos∠ABC=4+4﹣2×2×2×cos120°=12,
∴AC=2
 ,OC=
,OC= .
.∵直角三角形COD中,OD=
 =2,
=2,∴直角三角形GOD中,tan∠DGO=
 =
= .
.(Ⅲ)若G满足PC⊥面BGD,∵OG?平面BGD,∴PC⊥OG,且 PC=
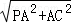 =
= .
.由△COG∽△PCA,可得
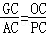 ,即
,即  ,解得GC=
,解得GC= ,
,∴PG=PC﹣GC=
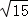 ﹣
﹣ =
=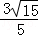 ,∴
,∴ =
=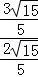 =
=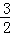 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,
中,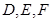 分别为棱
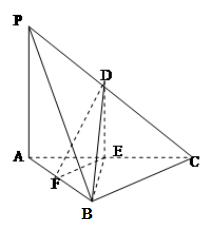
分别为棱 的中点,已知
的中点,已知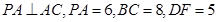 ,
,
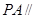 平面
平面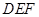 ;
;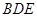
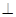 平面
平面 .
. 中,底面
中,底面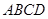 为平行四边形,
为平行四边形,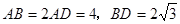
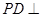 底面
底面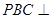 平面
平面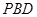 ;
;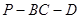 大小为
大小为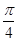 ,求
,求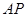 与平面
与平面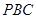 所成角的正弦值.
所成角的正弦值.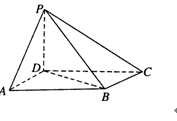
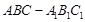 中,
中, 底面
底面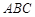 ,
,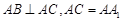 ,E、F分别是棱
,E、F分别是棱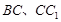 的中点.
的中点.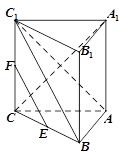
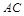 上的点
上的点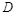 满足平面
满足平面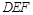 //平面
//平面 ,试确定点
,试确定点 中,底面
中,底面 是正方形,侧面
是正方形,侧面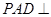 底面
底面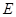 ,
,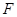 分别为
分别为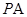 ,
,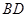 中点,
中点,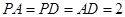 .
. 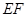 ∥平面
∥平面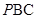 ;
;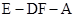 的余弦值;
的余弦值; 上是否存在一点
上是否存在一点 ,使
,使 平面
平面 ?若存在,指出点
?若存在,指出点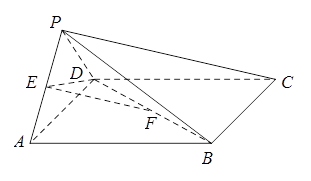
 中,底面
中,底面 是正方形,
是正方形,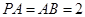 ,
,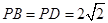 ,点
,点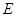 在
在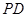 上,且
上,且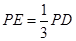 .
.
 平面
平面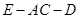 的余弦值;
的余弦值;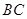 上存在点
上存在点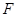 ,使
,使 ∥平面
∥平面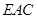 ,并求
,并求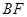 的长.
的长.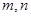 是两条不同的直线,
是两条不同的直线,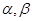 是两个不同的平面,给出下列条件,能得到
是两个不同的平面,给出下列条件,能得到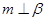 的是( )
的是( )