题目内容
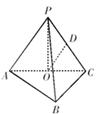
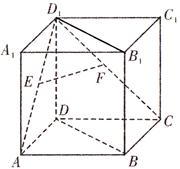
(满分14分)如图在三棱锥 中,
中,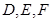 分别为棱
分别为棱 的中点,已知
的中点,已知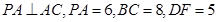 ,
,
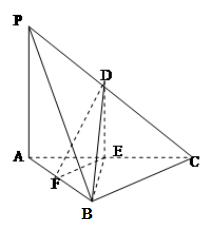
求证(1)直线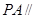 平面
平面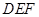 ;
;
(2)平面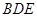
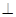 平面
平面 .
.
 中,
中,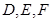 分别为棱
分别为棱 的中点,已知
的中点,已知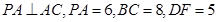 ,
,
求证(1)直线
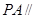 平面
平面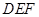 ;
;(2)平面
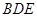
 平面
平面 .
.证明见解析.
试题分析:(1)本题证明线面平行,根据其判定定理,需要在平面
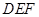 内找到一条与
内找到一条与 平行的直线,由于题中中点较多,容易看出
平行的直线,由于题中中点较多,容易看出 ,然后要交待
,然后要交待 在平面
在平面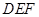 外,
外, 在平面
在平面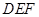 内,即可证得结论;(2)要证两平面垂直,一般要证明一个平面内有一条直线与另一个平面垂直,由(1)可得
内,即可证得结论;(2)要证两平面垂直,一般要证明一个平面内有一条直线与另一个平面垂直,由(1)可得 ,因此考虑能否证明
,因此考虑能否证明 与平面
与平面 内的另一条与
内的另一条与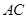 相交的直线垂直,由已知三条线段的长度,可用勾股定理证明
相交的直线垂直,由已知三条线段的长度,可用勾股定理证明 ,因此要找的两条相交直线就是
,因此要找的两条相交直线就是 ,由此可得线面垂直.
,由此可得线面垂直.试题解析:(1)由于
 分别是
分别是 的中点,则有
的中点,则有 ,又
,又 ,
, ,所以
,所以 .
.(2)由(1)
 ,又
,又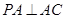 ,所以
,所以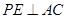 ,又
,又 是
是 中点,所以
中点,所以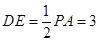 ,
, ,
, 又
又 ,所以
,所以 ,所以
,所以 ,
,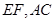 是平面
是平面 内两条相交直线,所以
内两条相交直线,所以 ,又
,又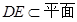
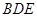 ,所以平面
,所以平面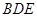
 平面
平面 .
.【考点】线面平行与面面垂直.

练习册系列答案
相关题目
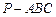 中,
中,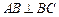 ,
,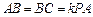 ,点
,点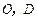 分别是
分别是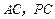 的中点,
的中点,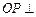 底面
底面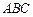 .
.
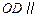 平面
平面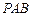 ;
;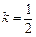 时,求直线
时,求直线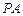 与平面
与平面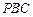 所成角的大小;
所成角的大小;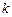 为何值时,
为何值时,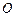 在平面
在平面 的重心?
的重心? 中,
中,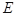 、
、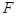 分别为
分别为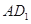 ,
,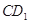 中点。
中点。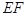 与
与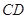 所成角的大小;
所成角的大小; 平面
平面 。
。
 中,
中, ,
,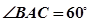 ,
,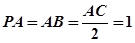 ,
, ,
, 分别是
分别是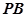 ,
,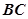 中点.
中点.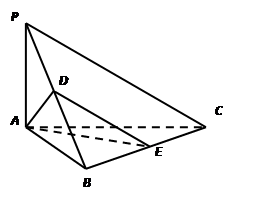
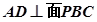 ;
;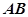 与平面
与平面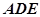 所成角的正弦值.
所成角的正弦值.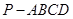 中,底面
中,底面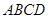 是正方形,侧棱
是正方形,侧棱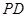 ⊥底面
⊥底面  ,
,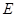 是
是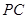 的中点,作
的中点,作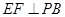 交
交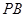 于点
于点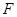 .
.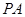
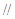 平面
平面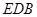 ;
;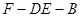 的正弦值.
的正弦值. 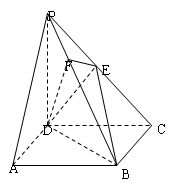
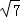 ,PA=
,PA=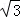 ,∠ABC=120°,G为线段PC上的点.
,∠ABC=120°,G为线段PC上的点.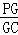 的值.
的值.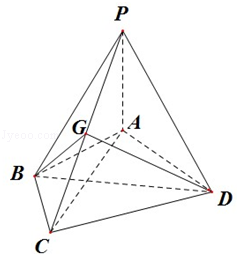
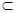 α,n∥α,则m∥n
α,n∥α,则m∥n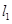 、
、 、
、 、
、 ,满足
,满足 ,
, ,
, ,则下列结论一定正确的是( )
,则下列结论一定正确的是( )
