题目内容
如图,在四棱锥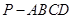 中,底面
中,底面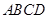 是正方形,侧面
是正方形,侧面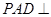 底面
底面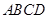 ,
,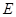 ,
,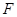 分别为
分别为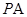 ,
,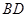 中点,
中点,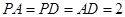 .
.
(Ⅰ)求证: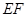 ∥平面
∥平面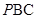 ;
;
(Ⅱ)求二面角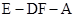 的余弦值;
的余弦值;
(Ⅲ)在棱 上是否存在一点
上是否存在一点 ,使
,使 平面
平面 ?若存在,指出点
?若存在,指出点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.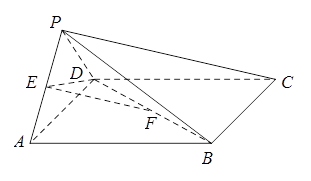
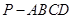 中,底面
中,底面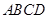 是正方形,侧面
是正方形,侧面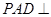 底面
底面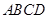 ,
,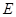 ,
,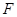 分别为
分别为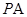 ,
,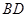 中点,
中点,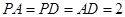 .
. (Ⅰ)求证:
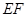 ∥平面
∥平面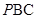 ;
;(Ⅱ)求二面角
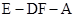 的余弦值;
的余弦值;(Ⅲ)在棱
 上是否存在一点
上是否存在一点 ,使
,使 平面
平面 ?若存在,指出点
?若存在,指出点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
(Ⅰ)详见解析,(Ⅱ)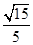 (Ⅲ)不存在.
(Ⅲ)不存在.
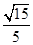 (Ⅲ)不存在.
(Ⅲ)不存在.试题分析:(Ⅰ)证明线面平行,关键在于找出线线平行.本题条件含中点,故从中位线上找线线平行.
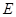 ,
,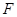 分别为
分别为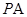 ,
,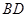 中点,在△
中点,在△ 中,
中,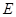 是
是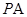 中点,
中点,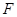 是
是 中点,所以
中点,所以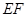 ∥
∥ .又因为
.又因为 平面
平面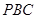 ,
,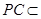 平面
平面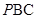 ,所以
,所以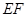 ∥平面
∥平面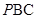 .(Ⅱ)求二面角的大小,有两个思路,一是作出二面角的平面角,这要用到三垂线定理及其逆定理,利用侧面
.(Ⅱ)求二面角的大小,有两个思路,一是作出二面角的平面角,这要用到三垂线定理及其逆定理,利用侧面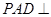 底面
底面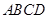 ,可得底面
,可得底面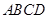 的垂线,再作DF的垂线,就可得二面角的平面角,二是利用空间向量求出大小.首先建立空间坐标系. 取
的垂线,再作DF的垂线,就可得二面角的平面角,二是利用空间向量求出大小.首先建立空间坐标系. 取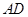 中点
中点 .由侧面
.由侧面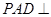 底面
底面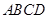 易得
易得 面
面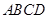 .以
.以 为原点,
为原点, 分别为
分别为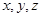 轴建立空间直角坐标系.再利用两平面法向量的夹角与二面角的平面角的关系,求出结果,(Ⅲ)存在性问题,一般从假设存在出发,构造等量关系,将存在是否转化为方程是否有解.
轴建立空间直角坐标系.再利用两平面法向量的夹角与二面角的平面角的关系,求出结果,(Ⅲ)存在性问题,一般从假设存在出发,构造等量关系,将存在是否转化为方程是否有解.
证明:(Ⅰ)如图,连结
 .
.因为底面
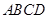 是正方形,
是正方形,所以
 与
与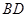 互相平分.
互相平分.又因为
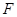 是
是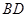 中点,
中点,所以
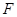 是
是 中点.
中点.在△
 中,
中,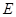 是
是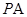 中点,
中点,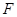 是
是 中点,
中点,所以
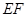 ∥
∥ .
.又因为
 平面
平面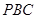 ,
,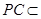 平面
平面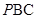 ,
,所以
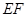 ∥平面
∥平面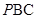 . 4分
. 4分(Ⅱ)取
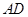 中点
中点 .在△
.在△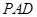 中,因为
中,因为 ,
,所以
 .
.因为面
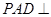 底面
底面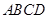 ,
,且面
 面
面 ,
,所以
 面
面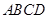 .
.因为
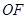
 平面
平面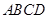
所以
 .
.又因为
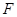 是
是 中点,
中点,所以
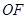
 .
.
如图,以
 为原点,
为原点, 分别为
分别为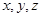 轴建立空间直角坐标系.
轴建立空间直角坐标系.因为
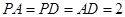 ,所以
,所以 ,则
,则 ,
, ,
,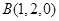 ,
,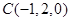 ,
, ,
,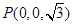 ,
, ,
, .
.于是
 ,
, ,
,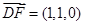 .
.因为
 面
面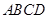 ,所以
,所以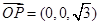 是平面
是平面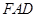 的一个法向量.
的一个法向量.设平面
 的一个法向量是
的一个法向量是 .
.因为
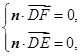 所以
所以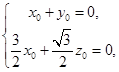 即
即
令
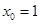 则
则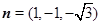 .
. 所以
 .
.由图可知,二面角
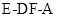 为锐角,所以二面角
为锐角,所以二面角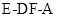 的余弦值为
的余弦值为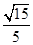 . 10分
. 10分(Ⅲ)假设在棱
 上存在一点
上存在一点 ,使
,使 面
面 .设
.设 ,
,则
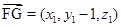 . 由(Ⅱ)可知平面
. 由(Ⅱ)可知平面 的一个法向量是
的一个法向量是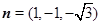 .
.因为
 面
面 ,所以
,所以 .
.于是,
 ,即
,即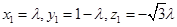 .
.又因为点
 在棱
在棱 上,所以
上,所以 与
与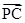 共线.
共线.因为
 ,
,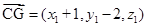 ,
,所以
 .
.所以
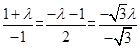 ,无解.
,无解.故在棱
 上不存在一点
上不存在一点 ,使
,使 面
面 成立. 14分
成立. 14分
练习册系列答案
相关题目
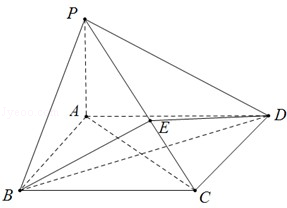
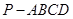 中,底面
中,底面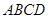 是正方形,侧棱
是正方形,侧棱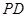 ⊥底面
⊥底面  ,
,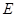 是
是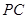 的中点,作
的中点,作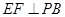 交
交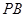 于点
于点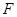 .
.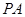
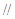 平面
平面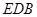 ;
;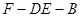 的正弦值.
的正弦值. 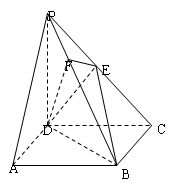
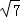 ,PA=
,PA=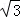 ,∠ABC=120°,G为线段PC上的点.
,∠ABC=120°,G为线段PC上的点.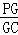 的值.
的值.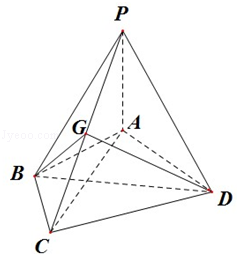
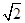 .
.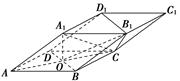
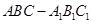 中,
中,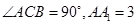 ,
,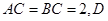 为
为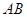 中点,
中点,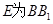 上一点,且
上一点,且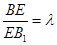 .
.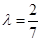 时,求证:
时,求证: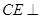 平面
平面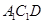 ;
; 与平面
与平面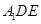 所成的角为
所成的角为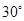 ,求
,求 的值.
的值.
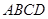 中,
中,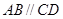 ,
,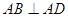 ,且
,且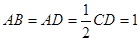 .
.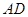 为一边向梯形外作正方形
为一边向梯形外作正方形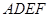 ,然后沿边
,然后沿边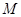 为
为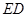 的中点,如图2.
的中点,如图2.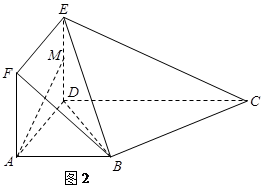
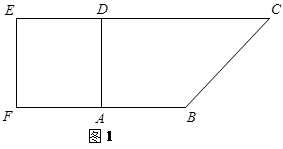
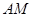 ∥平面
∥平面 ;
;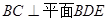 ;
;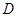 到平面
到平面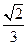
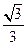
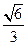
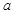 不平行于平面
不平行于平面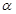 ,则下列结论成立的是( )
,则下列结论成立的是( )