题目内容
已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是( )
| A.AB∥m | B.AC⊥m |
| C.AB∥β | D.AC⊥β |
D
因为m∥α,m∥β,α∩β=l,所以m∥l.
因为AB∥l,所以AB∥m,故A一定正确.
因为AC⊥l,m∥l,所以AC⊥m,从而B一定正确.
因为AB∥l,l?β,AB?β.
所以AB∥β.故C也正确.
因为AC⊥l,当点C在平面α内时,AC⊥β成立,当点C不在平面α内时,AC⊥β不成立,故D不一定成立.
因为AB∥l,所以AB∥m,故A一定正确.
因为AC⊥l,m∥l,所以AC⊥m,从而B一定正确.
因为AB∥l,l?β,AB?β.
所以AB∥β.故C也正确.
因为AC⊥l,当点C在平面α内时,AC⊥β成立,当点C不在平面α内时,AC⊥β不成立,故D不一定成立.

练习册系列答案
相关题目
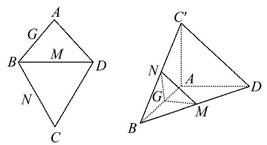
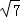 ,PA=
,PA=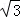 ,∠ABC=120°,G为线段PC上的点.
,∠ABC=120°,G为线段PC上的点.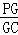 的值.
的值.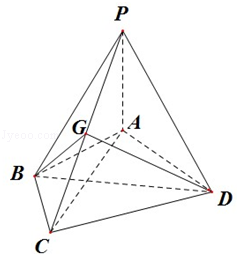
 底面是菱形,
底面是菱形, ,
, ,
, 分别是
分别是 的中点.
的中点.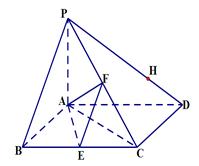
 ⊥平面
⊥平面 ;
;  是
是 上的动点,
上的动点, 与平面
与平面 ,求二面角
,求二面角 的正切值.
的正切值.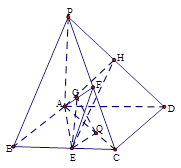
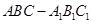 中,
中,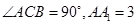 ,
,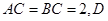 为
为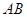 中点,
中点,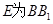 上一点,且
上一点,且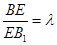 .
.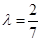 时,求证:
时,求证: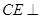 平面
平面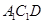 ;
; 与平面
与平面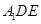 所成的角为
所成的角为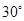 ,求
,求 的值.
的值.
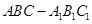 的底面边长是
的底面边长是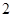 ,侧棱长是
,侧棱长是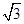 ,
,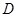 是
是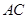 的中点.
的中点.
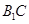 ∥平面
∥平面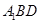 ;
;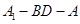 的大小;
的大小;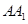 上是否存在一点
上是否存在一点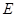 ,使得平面
,使得平面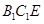
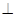 平面
平面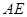 的长;若不存在,说明理由.
的长;若不存在,说明理由.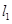 、
、 、
、 、
、 ,满足
,满足 ,
, ,
, ,则下列结论一定正确的是( )
,则下列结论一定正确的是( )

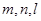 和两个不重合的平面
和两个不重合的平面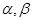 ,下列命题正确的是( )
,下列命题正确的是( )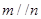 ,
,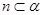 ,则
,则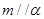
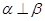 ,
,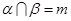 ,且
,且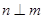 ,则
,则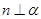
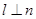 ,
,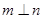 ,则
,则
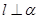 ,
,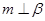 ,且
,且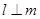 ,则
,则