题目内容
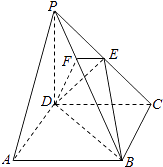
【题目】如图所示，直四棱柱ABCD﹣A1B1C1D1内接于半径为 
的半球O，四边形ABCD为正方形，则该四棱柱的体积最大时，AB的长是（ ） 
A.1
B.
C.
D.2
【答案】D
【解析】解：设AB=a，BB1=h， 则OB= 
a，连接OB1 ， OB，则OB2+BB12=OB12=3，
∴ 
=3，
∴a2=6﹣2h2 ，
故正四棱柱的体积是V=a2h=6h﹣2h3 ，
∴V′=6﹣6h2 ，
当0＜h＜1时，V′＞0，1＜h＜ 
时，V′＜0，
∴h=1时，该四棱柱的体积最大，此时AB=2．
故选：D．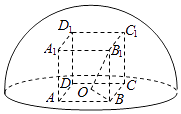
设AB=a，BB1=h，求出a2=6﹣2h2 ， 故正四棱柱的体积是V=a2h=6h﹣2h3 ， 利用导数，得到该正四棱柱体积的最大值，即可得出结论．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某高职院校进行自主招生文化素质考试，考试内容为语文、数学、英语三科，总分为200分.现从上线的考生中随机抽取20人，将其成绩用茎叶图记录如下：
男 | 女 | |||||||||||
15 | 6 | |||||||||||
5 | 4 | 16 | 3 | 5 | 8 | |||||||
8 | 2 | 17 | 2 | 3 | 6 | 8 | 8 | 8 | ||||
6 | 5 | 18 | 5 | 7 | ||||||||
19 | 2 | 3 | ||||||||||
（Ⅰ）计算上线考生中抽取的男生成绩的方差
；（结果精确到小数点后一位）
（Ⅱ）从上述茎叶图180分以上的考生中任选2人作为考生代表出席座谈会，求所选考生恰为一男一女的概率.
