题目内容
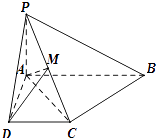
【题目】六个面都是平行四边形的四棱柱称为平行六面体.已知在平行四边形ABCD中(如图1),有AC2+BD2=2(AB2+AD2),则在平行六面体ABCD﹣A1B1C1D1中(如图2),AC12+BD12+CA12+DB12等于( ) 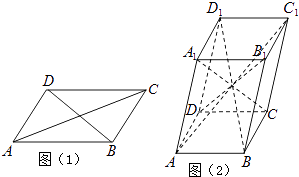
A.2(AB2+AD2+AA12)
B.3(AB2+AD2+AA12)
C.4(AB2+AD2+AA12)
D.4(AB2+AD2)
【答案】C
【解析】解:如图,平行六面体的各个面以及对角面都是平行四边形, 因此,在平行四边形ABCD中,AC2+BD2=2(AB2+AD2)…①;
在平行四边形ACC1A1中,A1C2+AC12=2(AC2+AA12)…②;
在平行四边形BDD1B1中,B1D2+BD12=2(BD2+BB12)…③;
②、③相加,得A1C2+AC12+B1D2+BD12=2(AC2+AA12)+2(BD2+BB12)…④
将①代入④,再结合AA1=BB1得,AC12+B1D2+A1C2+BD12=4(AB2+AD2+AA12)
故选C.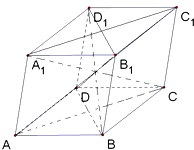
根据平行六面体的性质,可以得到它的各个面以及它的对角面均为平行四边形,多次使用已知条件中的定理,再将所得等式相加,可以计算出正确结论.

练习册系列答案
相关题目