题目内容
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F. 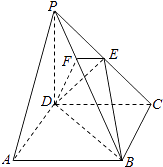
(1)证明PA∥平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C﹣PB﹣D的大小.
【答案】
(1)解:方法一:证明:连接AC,AC交BD于O,连接EO.
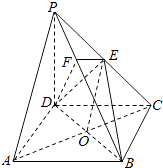
∵底面ABCD是正方形,∴点O是AC的中点
在△PAC中,EO是中位线,∴PA∥EO
而EO平面EDB且PA平面EDB,
所以,PA∥平面EDB
方法二:如图所示建立空间直角坐标系,D为坐标原点,设DC=a.
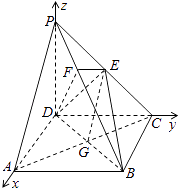
证明:连接AC,AC交BD于G,连接EG.
依题意得 ![]() .
.
∵底面ABCD是正方形,∴G是此正方形的中心,故点G的坐标为 ![]() 且
且 ![]() .
.
∴ ![]() ,这表明PA∥EG.
,这表明PA∥EG.
而EG平面EDB且PA平面EDB,∴PA∥平面EDB.
(2)解:证明:
∵PD⊥底面ABCD且DC底面ABCD,∴PD⊥DC
∵PD=DC,可知△PDC是等腰直角三角形,而DE是斜边PC的中线,
∴DE⊥PC.①
同样由PD⊥底面ABCD,得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC.
而DE平面PDC,∴BC⊥DE.②
由①和②推得DE⊥平面PBC.
而PB平面PBC,∴DE⊥PB
又EF⊥PB且DE∩EF=E,所以PB⊥平面EFD
证明;依题意得B(a,a,0), ![]() .
.
又 ![]() ,故
,故 ![]() .
.
∴PB⊥DE.
由已知EF⊥PB,且EF∩DE=E,所以PB⊥平面EFD.
(3)解:方法一:解:由(2)知,PB⊥DF,故∠EFD是二面角C﹣PB﹣D的平面角.
由(2)知,DE⊥EF,PD⊥DB.
设正方形ABCD的边长为a,
则 ![]()
![]() ,
, ![]()
![]() .
.
在Rt△PDB中, ![]() .
.
在Rt△EFD中, 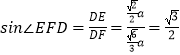 ,∴
,∴ ![]() .
.
所以,二面角C﹣PB﹣D的大小为 ![]() .
.
方法二:解:设点F的坐标为(x0,y0,z0), ![]() ,则(x0,y0,z0﹣a)=λ(a,a,﹣a).
,则(x0,y0,z0﹣a)=λ(a,a,﹣a).
从而x0=λa,y0=λa,z0=(1﹣λ)a.所以 ![]() .
.
由条件EF⊥PB知, ![]() ,即
,即 ![]() ,解得 /span>
,解得 /span>![]()
∴点F的坐标为 ![]() ,且
,且 ![]() ,
, ![]()
∴ ![]()
即PB⊥FD,故∠EFD是二面角C﹣PB﹣D的平面角.
∵ ![]() ,且
,且 ![]() ,
, ![]() ,
,
∴ 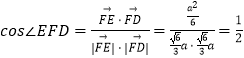 .
.
∴ ![]() .
.
所以,二面角C﹣PB﹣D的大小为 ![]()
【解析】法一:(1)连接AC,AC交BD于O,连接EO要证明PA∥平面EDB,只需证明直线PA平行平面EDB内的直线EO;(2)要证明PB⊥平面EFD,只需证明PB垂直平面EFD内的两条相交直线DE、EF,即可;(3)必须说明∠EFD是二面角C﹣PB﹣D的平面角,然后求二面角C﹣PB﹣D的大小.法二:如图所示建立空间直角坐标系,D为坐标原点,设DC=a.(1)连接AC,AC交BD于G,连接EG,求出 ![]() ,即可证明PA∥平面EDB;(2)证明EF⊥PB,
,即可证明PA∥平面EDB;(2)证明EF⊥PB, ![]() ,即可证明PB⊥平面EFD;(3)求出
,即可证明PB⊥平面EFD;(3)求出 ![]() ,利用
,利用 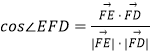 ,求二面角C﹣PB﹣D的大小.
,求二面角C﹣PB﹣D的大小.

【题目】某学校高一 、高二 、高三三个年级共有 ![]() 名教师,为调查他们的备课时间情况,通过分层
名教师,为调查他们的备课时间情况,通过分层
抽样获得了![]() 名教师一周的备课时间 ,数据如下表(单位 :小时):
名教师一周的备课时间 ,数据如下表(单位 :小时):
高一年级 |
|
|
|
|
| |||
高二年级 |
|
|
|
|
|
|
| |
高三年级 |
|
|
|
|
|
|
|
|
(1)试估计该校高三年级的教师人数 ;
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲 ,高二年级选出的人记为乙 ,求该周甲的备课时间不比乙的备课时间长的概率 ;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是![]() (单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为
(单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为![]() ,表格中的数据平均数记为
,表格中的数据平均数记为![]() ,试判断
,试判断![]() 与
与![]() 的大小. (结论不要求证明)
的大小. (结论不要求证明)