Question

【题目】(1)利用“五点法”画出函数在长度为一个周期的闭区间的简图.
(2)并说明该函数图象可由的图象经过怎样平移和伸缩变换得到的.

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

先列表如图确定的值,后描点并画图,利用“五点法”画出函数在长度为一个周期的闭区间的简图.
(2)依据的图象上所有的点向左平移个单位长度,，再把所得图象的横坐标伸长到原来的2倍(纵坐标不变),得到.

(1)先列表,后描点,并画图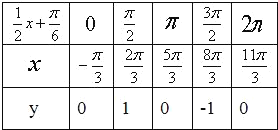


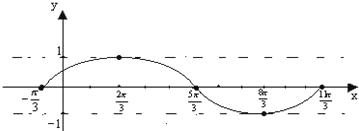
(2)把的图象上所有的点向左平移个单位长度,得到的图象,
再把所得图象的横坐标伸长到原来的2倍(纵坐标不变),得到的图象.
或把的图象横坐标伸长到原来的2倍(纵坐标不变),得到的图象.
再把所得图象上所有的点向左平移个单位长度,得到,

即的图象.

本题考查五点法作函数的图象,函数的图象变换,考查计算能力,是基础题.