Question

【题目】A，B，C，D是空间不共面的四点，它们到平面a的距离之比依次为1：1：1：2，则满足条件的平面a的个数是：

A. 1 B. 4 C. 7 D. 8.

Answer 1

【答案】D

【解析】

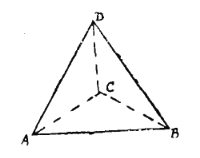
解：∵A，B，C，D四点不共面，故可视为一个四面体的四个顶点.（如图）

（1）当A在平面a的一侧，而B、c、d在平面a的另一侧时，可在AB、AC、AD上各取E，F，G，使 ，

则过不共线的三点E，F，G所确定的平面，即为满足条件的平面.

如将A点分别换作B，C，D同样可求得满足条件的平面.故这一类的平面共有四个.

（2）当A，B两点在平面a的一侧，而C，D两点在平面a的另一侧时，可在，，AD上各取M，N，P使，，.

则过不共线的三点M，N，P的平面亦为满足条件的平面.当B，C两点与A，D两点，A，C两点与B，D两点各分別在平面的两侧时，同理可求得满足条件的平面.故这一类的平面共有三个.

（3）当四点均在平面a的同一侧时，只要延长DA，DB，DC，到A’，B’，C’，使

.

这样过A’，B’，C’，所确定的平面亦为满足条件的平面，但这样的平面只有一个.

综上所述，4+3+1=8，满足条件的平面只有8个.故选D..